
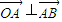 ,点A(4,-3),B点在第一象限且到x轴的距离为5.
,点A(4,-3),B点在第一象限且到x轴的距离为5.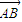 的坐标及OB所在的直线方程;
的坐标及OB所在的直线方程;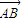 为方向向量且过(0,a)点,问是否存在实数a,使得椭圆
为方向向量且过(0,a)点,问是否存在实数a,使得椭圆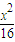 +y2=1上有两个不同的点关于直线l对称.若不存在,请说明理由; 存在请求出实数a的取值范围.
+y2=1上有两个不同的点关于直线l对称.若不存在,请说明理由; 存在请求出实数a的取值范围.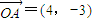 ,
, ,由
,由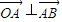 ,可得4(x-4)-24=0,x=10,由此能够求出向量
,可得4(x-4)-24=0,x=10,由此能够求出向量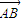 的坐标及OB所在的直线方程.
的坐标及OB所在的直线方程.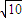 .由方程
.由方程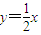 知
知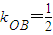 ,由此能够推导出所求圆的方程.
,由此能够推导出所求圆的方程.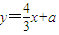 ,可设直线AB的方程为
,可设直线AB的方程为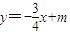 ,将其与已知椭圆方程联立得5x2-12mx+8m2-8=0.再由韦达定理进行求解.
,将其与已知椭圆方程联立得5x2-12mx+8m2-8=0.再由韦达定理进行求解.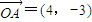 ,
,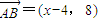 ,
,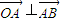 ,可得
,可得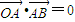 ,
,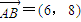 ,
,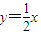 (5分)
(5分)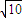 .
.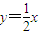 知
知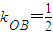 ,
,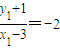 ,又点
,又点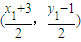 在
在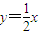 上
上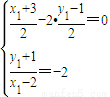 ,∴
,∴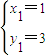 ,
,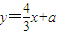 ,
,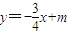
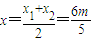 ,
,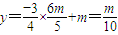 .(12分)
.(12分)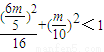 ,
,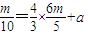 ,
,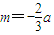 代入m2<10
代入m2<10 ,
,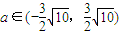 .(16分)
.(16分)

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
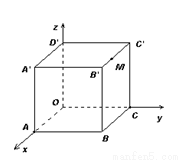
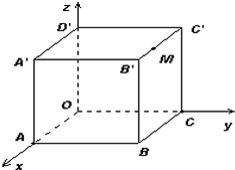 11、如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
11、如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修2 2.3空间直角坐标系练习卷(解析版) 题型:填空题
如右图,棱长为3a正方体OABC-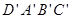 ,点M在
,点M在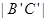 上,且
上,且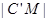
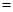 2
2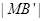 ,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .
,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .
查看答案和解析>>
科目:高中数学 来源:2012年人教B版高中数学必修2 2.4空间直角坐标系练习卷(解析版) 题型:填空题
如右图,棱长为3a正方体OABC-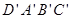 ,点M在
,点M在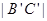 上,且
上,且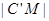
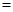 2
2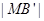 ,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
.
,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
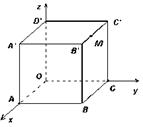
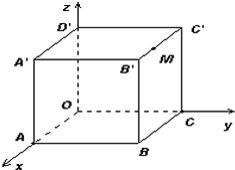 如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.
如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com