
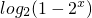 ,试求函数f(x)的反函数f-1(x),并证明f-1(x)∈M;
,试求函数f(x)的反函数f-1(x),并证明f-1(x)∈M;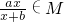 (a,b为常数且a>0),求使f(x)<1成立的x的取值范围.
(a,b为常数且a>0),求使f(x)<1成立的x的取值范围.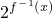 )=log2(1-(1-2x))=x…(9分)
)=log2(1-(1-2x))=x…(9分)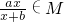 ,所以f(f(x))=x对定义域内一切x恒成立,
,所以f(f(x))=x对定义域内一切x恒成立,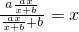
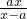 <1即
<1即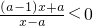 …(13分)
…(13分) <0,所以x∈(-∞,1)…(14分)
<0,所以x∈(-∞,1)…(14分)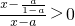 且a<
且a<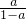 ,所以x∈(-∞,a)∪(
,所以x∈(-∞,a)∪(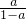 ,+∞)…(16分)
,+∞)…(16分)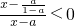 且a>
且a>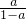 ,所以x∈(
,所以x∈(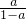 ,a)…(18分)
,a)…(18分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
A、g(x)=f(
| ||
| B、g(x)=f(3-x) | ||
| C、g(x)=f(-3-x) | ||
| D、g(x)=f(6-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax | x+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ax | x+b |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三第五次质量检测文科数学试卷(解析版) 题型:选择题
设函数y=f(x)与函数y=g(x)的图象如右图所示,则函数y= f(x)·g(x)的图象可能是


查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三第五次质量检测文科数学试卷(解析版) 题型:选择题
设函数y=f(x)与函数y=g(x)的图象如右图所示,则函数y= f(x)·g(x)的图象可能是


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com