
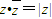 不成立
不成立

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有查看答案和解析>>
科目:高中数学 来源:2011届山东省济宁一中高三第三次月考理科数学卷 题型:填空题
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 .
①动点A′在平面ABC上的射影在线段AF上;
②三棱锥A′—FED的体积有最大值;
③恒有平面A′GF⊥平面BCED;
④异面直线A′E与BD不可能互相垂直;
⑤异面直线FE与A′D所成角的取值范围是
查看答案和解析>>
科目:高中数学 来源:2011届河南省许昌市三校高三上学期期末数学理卷 题型:填空题
如图,边长为a的正△ABC的中 线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号).
线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号).
①动点A′在平面ABC上的射影在线段AF上;
②三棱锥A′—FED的体积有最大值;
③恒有平面A′GF⊥平面BCED;
④异面直线A′E与BD不可能互相垂直;
⑤异面直线FE与A′D所成角的取值范围是 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省许昌市三校高三上学期期末数学理卷 题型:填空题
如图,边长为a的正△ABC的中 线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
(只需填上正确命题的序号).
线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
(只需填上正确命题的序号).
①动点A′在平面ABC上的射影在线段AF上;
②三棱锥A′—FED的体积有最大值;
③恒有平面A′GF⊥平面BCED;
④异面直线A′E与BD不可能互相垂直;
⑤异面直线FE与A′D所成角的取值范围是 .
.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省高三第三次月考理科数学卷 题型:填空题
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 .

①动点A′在平面ABC上的射影在线段AF上;
②三棱锥A′—FED的体积有最大值;
③恒有平面A′GF⊥平面BCED;
④异面直线A′E与BD不可能互相垂直;
⑤异面直线FE与A′D所成角的取值范围是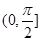
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com