解:(1)由a
n+1=2(

)
2a
n得:
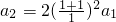
?

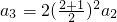
?

…

?

将这n-1个式子相乘,得a
n=2
n-1n
2a
1=2
n•n
2,
(2)∵b
n=(An
2+Bn+C)•2
n
∴b
n+1=(A(n+1)
2+B(n+1)+C)•2
n+1
∴b
n+1-b
n=(A(n+1)
2+B(n+1)+C)•2
n+1-(An
2+Bn+C)•2
n
=(An
2+(4A+B)n+2A+2B+C)•2
n
若a
n=b
n+1-b
n成立,则2
n•n
2=(An
2+(4A+B)n+2A+2B+C)•2
n对一切正整数n都成立
∴An
2+(4A+B)n+2A+2B+C=n
2
∴

?A=1,B=-4,C=6;
(3)用数学归纳法进行证明:
当n=1时,a
1=2≤(1
2-2×1+2)•2
1:=2,式子成立
当n≥2时,设n=k时不等式成立,
即a
1+a
2+…+a
k≤(k
2-2k+2)•2
k成立,则
a
1+a
2+…+a
k+a
k+1≤(k
2-2k+2)•2
k+2
k+1•(k+1)
2而(k
2-2k+2)•2
k+2
k+1•(k+1)
2=2
k+1[(

k
2-k+1)+(k
2+2k+1)]
=2
k+1(

k
2+k+2)
并且2
k+1(

k
2+k+2)≤((k+1)
2-2(k+1)+2)•2
k+1,
∴a
1+a
2+…+a
k+a
k+1)≤((k+1)
2-2(k+1)+2)•2
k+1
即n=k+1时不等式成立,
综上所述,可得对任意 n∈N
*,a
1+a
2+…+a
n≤(n
2-2n+2)•2
n 总成立
分析:(1)用n=1、n=2、n=3、…,一共n-1个值代入式子:a
n+1=2(

)
2a
n得到n-1个等式,将此n-1个等式相乘,就可以得到a
n=2
n-1n
2a
1=2
n•n
2;
(2)根据b
n=(An
2+Bn+C)•2
n,得到b
n+1=(A(n+1)
2+B(n+1)+C)•2
n+1,再将b
n+1-b
n进行化简,整理得
(An
2+(4A+B)n+2A+2B+C)•2
n,最后根据An
2+(4A+B)n+2A+2B+C=2
n恒等,采用比较系数法,可得A、B、C的值;
(3)采用数学归纳法,先验证n=1时不等式的等号成立,然后假设n=k(n≥2)时不等式成立,即a
1+a
2+…+a
k≤(k
2-2k+2)•2
k,采用放缩的方法可以证出n=k+1时,a
1+a
2+…+a
k+a
k+1)≤((k+1)
2-2(k+1)+2)•2
k+1也成立,因此可以得出结论对所有的正整数n,不等式都能成立.
点评:本题主要考查了数列的递推式、数学归纳法和不等式的证明等知识点,是一道难题.注意解题过程中数学归纳的一般方法和不等式放缩的技巧,以达到证明的目的.

 )2an
)2an )2an得:
)2an得: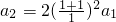 ?
?
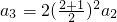 ?
?
 ?
?
 ?A=1,B=-4,C=6;
?A=1,B=-4,C=6; k2-k+1)+(k2+2k+1)]
k2-k+1)+(k2+2k+1)] k2+k+2)
k2+k+2) k2+k+2)≤((k+1)2-2(k+1)+2)•2k+1,
k2+k+2)≤((k+1)2-2(k+1)+2)•2k+1, )2an得到n-1个等式,将此n-1个等式相乘,就可以得到an=2n-1n2a1=2n•n2;
)2an得到n-1个等式,将此n-1个等式相乘,就可以得到an=2n-1n2a1=2n•n2;
