
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率
(1) .(2)
.(2)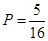 .
.
解析试题分析:古典概型概率的计算问题,需要计算基本事件空间总数及事件发生所包含的基本事件数,常用方法有“树图法”、“坐标法”,本题可以利用两种方法予以解答.
试题解析:解法一:利用树状图可以列出从甲、乙两个盒子中各取出1个球的所有可能结果: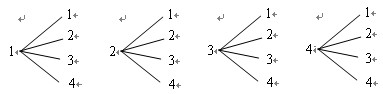
可以看出,试验的所有可能结果数为16种. 4分
(1)所取两个小球上的标号为相邻整数的结果有1-2,2-1,2-3,3-2,3-4,
4-3,共6种. 6分
故所求概率 .
.
答:取出的两个小球上的标号为相邻整数的概率为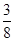 . 8分
. 8分
(2)所取两个球上的数字和能被3整除的结果有1-2,2-1,2-4,3-3,4-2,共5种. 10分
故所求概率为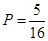 .
.
答:取出的两个小球上的标号之和能被3整除的概率为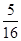 . 12分
. 12分
解法二:设从甲、乙两个盒子中各取1个球,其数字分别为 ,用
,用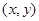 表示抽取结果,则所有可能有
表示抽取结果,则所有可能有 ,
,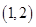 ,
,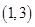 ,
,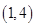 ,
,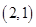 ,
,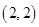 ,
, ,
,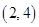 ,
,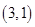 ,
, ,
,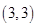 ,
, ,
,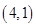 ,
, ,
,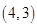 ,
,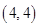 ,共16种. 4分
,共16种. 4分
(1)所取两个小球上的数字为相邻整数的结果有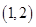 ,
, 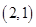 ,
,  ,
, ,
,  ,
, 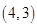 ,共6种. 6分
,共6种. 6分
故所求概率 .
.
答:取出的两个小球上的标号为相邻整数的概率为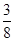 . 8分
. 8分
(2)所取两个球上的数字和能被3整除的结果有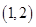 ,
, 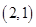 ,
, 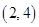 ,
, 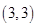 ,
,  ,共5种. 10分
,共5种. 10分
故所求概率为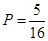 .
.
答:取出的两个小球上的标号之和能被3整除的概率为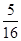 . 12分
. 12分
考点:古典概型概率的计算


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
淮南八公山某种豆腐食品是经过A、B、C三道工序加工而成的,A、B、C工序的产品合格率分别为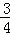 、
、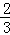 、
、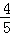 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两次合格为二等品;其它的为废品,不进入市场.
(Ⅰ)正式生产前先试生产2袋食品,求这2袋食品都为废品的概率;
(Ⅱ)设ξ为加工工序中产品合格的次数,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成社团指导小组,有关数据见下表:(单位:人)
(1)求 的值;
的值;
(2)若从“动漫”与“话剧”社团已抽取的人中选2人担任指导小组组长,求这2人分别来自这两个社团的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若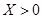 就去打球;若
就去打球;若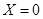 就去唱歌;若
就去唱歌;若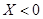 就去下棋.
就去下棋.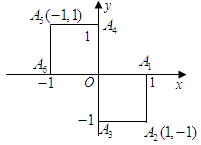
(Ⅰ) 写出数量积X的所有可能取值;
(Ⅱ)分别求小波去下棋的概率和不去唱歌的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
| 合格的概率 |  |  |  |  |
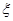 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求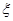 的分布列及期望
的分布列及期望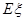 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某校在一次考试中,5名学生的数学和物理成绩如下表:
| 学生的编号i | 1 | 2 | 3 | 4 | 5 |
| 数学成绩x | 80 | 75 | 70 | 65 | 60 |
| 物理成绩y | 70 | 66 | 68 | 64 | 62 |
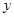 关于
关于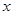 的线性回归方程
的线性回归方程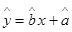 ,
,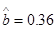
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:
| 视力数据 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
| 人数 | | | | | 2 | | 2 | | 2 | 1 | | 1 | | |
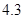 、
、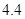 、
、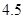 、
、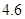 、
、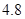 .若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于
.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于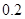 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两队参加知识竞赛,每队 人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为
人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为 ,乙队中
,乙队中 人答对的概率分别为
人答对的概率分别为 且各人正确与否相互之间没有影响.用
且各人正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分.
(Ⅰ)求随机变量 分布列
分布列
(Ⅱ)用 表示“甲、乙两个队总得分之和等于
表示“甲、乙两个队总得分之和等于 ”这一事件,用
”这一事件,用 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com