
观察下列等式
1=1
2+3+4=9
3+4+5+6+7=25
4+5+6+7+8+9+10=49
照此规律,第 个等式为 .
个等式为 .
科目:高中数学 来源: 题型:单选题
已知变量x与y正相关,且由观测数据算得样本平均数线性回归方程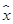 =3,
=3,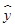 =3.5,则由该观测数据算得的线性回归方程可能是( )
=3.5,则由该观测数据算得的线性回归方程可能是( )
A.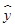 =-2x+9.5 =-2x+9.5 | B.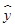 =2x-2.4 =2x-2.4 |
C.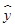 =0.4x+2.3 =0.4x+2.3 | D.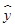 =-0.3x+4.4 =-0.3x+4.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,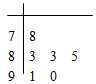
给出关于该同学数学成绩的以下说法:
①中位数为83; ②众数为83; ③平均数为85; ④极差为12.
其中,正确说法的序号是( )
| A.①② | B.②③ | C.③④ | D.②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知函数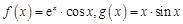 ,其中
,其中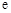 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线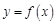 在点
在点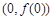 处的切线方程;
处的切线方程;
(Ⅱ)若对任意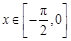 ,不等式
,不等式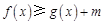 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)试探究当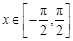 时,方程
时,方程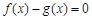 解的个数,并说明理由.
解的个数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com