
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的极值点;
的极值点;
(Ⅱ)求函数 的单调区间.
的单调区间.
解:
(Ⅰ)当 时,
时,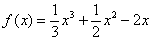 .
.
所以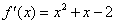 .
.
令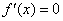 得,
得, .
.
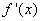 与
与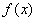 变化规律如下表:
变化规律如下表:
| x | (-∞,-2) | -2 | (-2,1) | 1 | (1,+∞) |
|
| + | 0 | - | 0 | + |
|
| ↑ | 极大值 | ↓ | 极小值 | ↑ |
所以函数 的极大值点为-2,极小值点为1.
的极大值点为-2,极小值点为1.
(Ⅱ)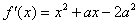
令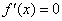 ,得
,得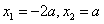 .
.
(1)当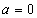 时,
时,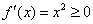 ,
,  在的单调递增区间为
在的单调递增区间为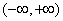
(2)当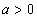 时,
时,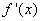 与
与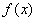 变化规律如下表:
变化规律如下表:
| x | (-∞,-2a) | -2a | (-2a,a) | a | (a,+∞) |
|
| + | 0 | - | 0 | + |
|
| ↑ | 极大值 | ↓ | 极小值 | ↑ |
所以f(x)的增区间是(-∞,-2a)和(a,+∞),减区间是(-2a,a)------- 12分
(3)当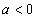 时,
时,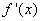 与
与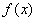 变化规律如下表:
变化规律如下表:
| x | (-∞,a) | a | (a,-2a) | -2a | (-2a,+∞) |
|
| + | 0 | - | 0 | + |
|
| ↑ | 极大值 | ↓ | 极小值 | ↑ |
所以f(x)的增区间是(-∞,a)和(-2a,+∞),减区间是(a,-2a)
综上所述,当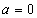 时,
时,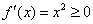 ,f(x)在R上单调递增;
,f(x)在R上单调递增;
当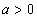 时,f(x)的增区间是(-∞,-2a)和(a,+∞),减区间是(-2a,a);
时,f(x)的增区间是(-∞,-2a)和(a,+∞),减区间是(-2a,a);
当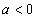 时,f(x)的增区间是(-∞,a)和(-2a,+∞),减区间是(a,-2a).--14分
时,f(x)的增区间是(-∞,a)和(-2a,+∞),减区间是(a,-2a).--14分
(无综上所述不扣分)


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014-2015学年湖南省名校高二上学期期末考试文科数学试卷(解析版) 题型:填空题
2014年一轮又一轮的寒潮席卷全国.某商场为了了解某品牌羽绒服的月销售量y(件)与月平均气温x(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气
温,数据如下表:
月平均气温x(℃) | 17 | 13 | 8 | 2 |
月销售量y(件) | 24 | 33 | 40 | 55 |
由表中数据算出线性回归方程=bx+a中的b≈-2.气象部门预测下个月的平均气温约为6℃,据此估计,该商场下个月羽绒服的销售量约为________件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com