
某工厂有A、B两种配件生产甲、乙两种产品,每生产一种甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
每天生产甲产品 件,乙产品
件,乙产品 件时,工厂可获得最大利润
件时,工厂可获得最大利润 万元.
万元.
解析试题分析:由题意可知,若设甲、乙两种产品分别生产 ,
, 件,工厂获得的利润为
件,工厂获得的利润为 ,则可得
,则可得 ,
, ,从而问题就等价于在线性约束条件
,从而问题就等价于在线性约束条件 下,求线性目标函数
下,求线性目标函数 ,作出不等式组所表示的可行域,在作出直线
,作出不等式组所表示的可行域,在作出直线 ,通过平移直线,即可知,使目标函数取得最大值的点为直线
,通过平移直线,即可知,使目标函数取得最大值的点为直线 与直线
与直线 的交点
的交点 ,从而得到每天生产甲产品
,从而得到每天生产甲产品 件,乙产品
件,乙产品 件时,工厂可获得最大利润
件时,工厂可获得最大利润 万元.
万元.
.
试题解析:设甲、乙两种产品分别生产 ,
, 件,工厂获得的利润为
件,工厂获得的利润为 ,由题意可得 2分
,由题意可得 2分 , 5分 目标函数为
, 5分 目标函数为 , 6分
, 6分
作出线性约束条件表示的可行域如下图所示:
把 变形为
变形为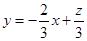 ,这是斜率为
,这是斜率为 ,在
,在 轴上截距为
轴上截距为 的直线,当
的直线,当 变化时,可以得到一族相互平行的直线,当截距
变化时,可以得到一族相互平行的直线,当截距 最大时,
最大时, 取得最大值,由上图可以看出,
取得最大值,由上图可以看出,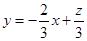 ,当直线
,当直线 与直线
与直线 的交点
的交点 时,截距
时,截距 的值最大,最大值为
的值最大,最大值为 ,此时
,此时 ,∴每天生产甲产品
,∴每天生产甲产品 件,乙产品
件,乙产品 件时,工厂可获得最大利润
件时,工厂可获得最大利润 万元. 12分
万元. 12分
考点:线性规划的运用.


科目:高中数学 来源: 题型:填空题
在平面直角坐标系中, 点集A="{(x," y)|  }, 点集B="{(x," y)|
}, 点集B="{(x," y)|  , 则点集M="{(x," y)|x=x
, 则点集M="{(x," y)|x=x +x
+x , y=y
, y=y +y
+y , (x
, (x , y
, y )
) A, (x
A, (x , y
, y )
) B}所表示的区域的面积为_____________.
B}所表示的区域的面积为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
对一切实数x,不等式x2+a|x|+1≥0恒成立,则实数a的取值范围是( )
| A.[-2,+∞) | B.(-∞,-2) |
| C.[-2,2] | D.[0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com