变量x、y满足
(1)设z＝
，求z的最小值；
(2)设z＝x2＋y2，求z的取值范围．
（1）
；（2）
.
解析试题分析： 由题意画出可行域，分别求出可行域各顶点
、
、
坐标.（1）将所求目标函数
构造为
，此时
可以看作是可行域内的点与原点连成直线的斜率的最小值，由于可行域范围在第一象限内，所以可行域内的点与原点连线中倾斜角最小的为
，故
，再由顶点坐标可求出的最小值；（2）将目标函数
构造为
，此时可以看作是可行域内的点与原点之间距离的范围，经查验比较可得
，
，通过计算
、
的值可以求出所求的取值范围.提示：在解决此类线性规划问题中，常常把目标函数构造出斜截式的直线方程
、过原点直线的斜率
、与某一定点间的距离
等等，再通过求截距、斜率、距离来求出目标函数的值.
试题解析：由约束条件
，作出
可行域如图所示.
3分
由
，解得
由
，解得
由
，解得
. 6分
（1）因为
，所以的值即是可行域中的点与原点
连线的斜率.
观察图形可知
9分
（2）的几何意义是可行域上的点到原点的距离的平方，
结合图形可知，可行域上的点到原点的距离中，
，
，
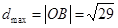所以所求的取值范围为.
考点：1线性规划问题；2.斜率的计算.
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案科目：高中数学 来源： 题型：解答题
某工厂有A、B两种配件生产甲、乙两种产品，每生产一种甲产品使用4个A配件耗时1h，每生产一件乙产品使用4个B配件耗时2h，该厂每天最多可从配件厂获得16个A配件和12个B配件，按每天8h计算，若生产一件甲产品获利2万元，生产一件乙产品获利3万元，采用哪种生产安排利润最大？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量．记一天中从甲地去乙地的旅客人数不超过900的概率为p0.
(1)求p0的值；(参考数据：若X～N(μ，σ2)，有P(μ－σ＜X≤μ＋σ)＝0.682 6，P(μ－2σ＜X≤μ＋2σ)＝0.954 4，P(μ－3σ＜X≤μ＋3σ)＝0.997 4)
(2)某客运公司用A、B两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次．A、B两种车辆的载客量分别为36人和60人，从甲地去乙地的营运成本分别为1 600元/辆和2 400元/辆．公司拟组建一个不超过21辆车的客运车队，并要求B型车不多于A型车7辆．若每天要以不小于p0的概率运完从甲地去乙地的旅客，且使公司从甲地去乙地的营运成本最小，那么应配备A型车、B型车各多少辆？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知x，y满足约束条件
，试求解下列问题．
(1)z＝
的最大值和最小值；
(2)z＝
的最大值和最小值；
(3)z＝|3x＋4y＋3|的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知关于
的二次函数
（1）设集合
和
分别从集合
和
中随机取一个数作为
和
，求函数
在区间
上是增函数的概率.
（2）设点（a,b）是区域
内的随机点，求函数
在区间上是增函数的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
要证a2+b2-1-a2b2≤0,只要证 ( )
| A．2ab-1-a2b2≤0 |
B．a2+b2-1- ≤0 |
C． -1-a2b2≤0 |
| D．(a2-1) (b2-1)≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
,
上的函数
满足：
；
，且
，有
.
，则k的最小值为（ ）
满足约束条件
，则目标函数
的最大值为 .