
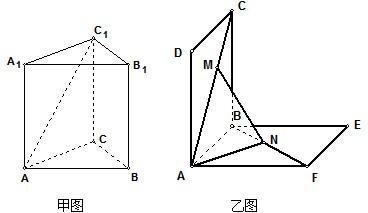
20.(乙)如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
SA=AB=BC=1,AD=![]() .
.
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
20.(乙)本小题主要考查线面关系和棱锥体积计算,以及空间想象能力和逻辑推理能力.

解:
(Ⅰ)直角梯形ABCD的面积是
M底面=![]() (BC+AD)·AB=
(BC+AD)·AB=![]() 1=
1=![]() .
.
∴四棱锥S-ABCD的体积是
V=![]() ×SA×M底面
×SA×M底面
=![]() ×1×
×1×![]()
=![]() .
.
(Ⅱ)延长BA、CD相交于点E,连结SE,则SE是所求二面角的棱.
∵AD∥BC,BC=2AD.
∴EA=AB=SA,∴SE⊥SB.
∵SA⊥面ABCD.得面SEB⊥面EBC,EB是交线.
又BC⊥EB,∴BC⊥面SEB,故SB是CS在面SEB上的射影,
∴CS⊥SE.
所以∠BSC是所求二面角的平面角.
∵SB=![]() =
=![]() ,BC=1,BC⊥SB.
,BC=1,BC⊥SB.
∴tanBSC=![]() =
=![]() .
.
即所求二面角的正切值为![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
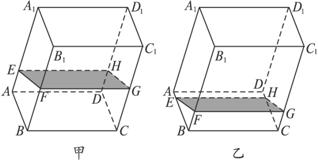
①水的部分始终呈棱柱状;
②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行;
④当容器倾斜如图乙时,EF·BF是定值.
其中正确命题的序号是_______________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
20.(乙)如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
SA=AB=BC=1,AD=![]() .
.
(Ⅰ)求四棱锥S-ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
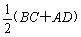
查看答案和解析>>
科目:高中数学 来源:2002年天津市高考数学试卷(理科)(解析版) 题型:解答题
 .
. .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com