

 an+12-
an+12- an+1,分两种情况讨论:①当n≥2时,利用an=Sn-Sn-1,解得an+1-an=
an+1,分两种情况讨论:①当n≥2时,利用an=Sn-Sn-1,解得an+1-an= ;②当n=1时,解得a2-a1=
;②当n=1时,解得a2-a1= ,即为an+1-an=
,即为an+1-an= ,故得到数列的通项公式为an=
,故得到数列的通项公式为an=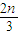 .
.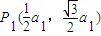 ,P1在曲线上,代入y2=x(y≥0)
,P1在曲线上,代入y2=x(y≥0)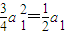 ,∵a1>0,∴a1=
,∵a1>0,∴a1= ;
;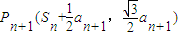
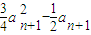 ,
,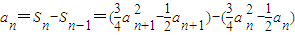
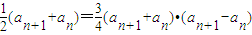
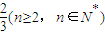
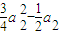 ,∴
,∴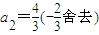
 ,
,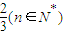
 .公差为
.公差为 的等差数列,即an=
的等差数列,即an= n;
n;

科目:高中数学 来源: 题型:
 如图,曲线y=f(x)上任一点P的切线PQ交x轴于Q,过P作PT垂直于x轴于T,若△PTQ的面积为
如图,曲线y=f(x)上任一点P的切线PQ交x轴于Q,过P作PT垂直于x轴于T,若△PTQ的面积为| 1 |
| 2 |
| A、y=y′ |
| B、y=-y′ |
| C、y=y′2 |
| D、y2=y′ |
查看答案和解析>>
科目:高中数学 来源: 题型:
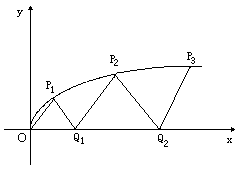
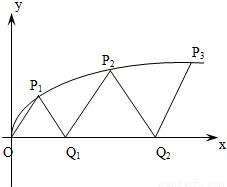
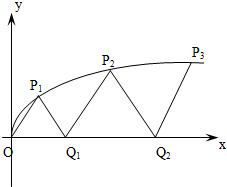 如图,曲线y2=x(y≥0)上的点Pi与x轴的正半轴上的点Qi及原点O构成一系列正三角形△OP1Q1,△Q1P2Q2,…△Qn-1PnQn…设正三角形Qn-1PnQn的边长为an,n∈N﹡(记Q0为O),Qn(Sn,0).
如图,曲线y2=x(y≥0)上的点Pi与x轴的正半轴上的点Qi及原点O构成一系列正三角形△OP1Q1,△Q1P2Q2,…△Qn-1PnQn…设正三角形Qn-1PnQn的边长为an,n∈N﹡(记Q0为O),Qn(Sn,0).查看答案和解析>>
科目:高中数学 来源:南通高考密卷·数学(理) 题型:044
如图,曲线y2=x(y≥0)上的点Pi与x轴的正半轴上的点Qi及原点O构成一系列正三角形:△OP1Q1,△Q1P2Q2,…,△Qn-1PnQn,….设正三角形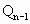 PnQn的边长为an,n∈N*(记Q0为O),Qn(Sn,0).
PnQn的边长为an,n∈N*(记Q0为O),Qn(Sn,0).
(1)求a1的值;
(2)求数列{an}的通项公式an;
(3)求证:当n≥2时,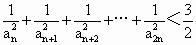 .
.
查看答案和解析>>
科目:高中数学 来源:2010年河南省郑州47中高考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com