
| | 带菌头数 | 不带菌头数 | 合计 |
| 屠宰场 | 8 | 32 | 40 |
| 零售店 | 14 | 18 | 32 |
| 合计 | 22 | 50 | 72 |
 )
) 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源:不详 题型:单选题
 x+1上,则这组样本数据的样本相关系数为
x+1上,则这组样本数据的样本相关系数为 | A.-1 | B.0 | C. | D.1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.人的身高和体重 |
| B.降雪量和交通事故发生率 |
| C.匀速行驶的车辆的行驶距离和时间 |
| D.每亩施用肥料量和粮食亩产量 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.若K2的观测值为k=6.635,在犯错误的概率不超过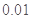 的前提下认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病; 的前提下认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病; |
B.由独立性检验可知,在犯错误的概率不超过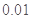 的前提下认为吸烟与患肺病有关系,我们说某人吸烟,那么他有99%的可能患有肺病;[ 的前提下认为吸烟与患肺病有关系,我们说某人吸烟,那么他有99%的可能患有肺病;[ |
C.若从统计量中求出在犯错误的概率不超过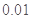 的前提下认为吸烟与 的前提下认为吸烟与 患肺病有关系,是指有1% 的可能性使得判断出现错误; |
| D.以上三种说法都不正确. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (公顷)与当地气温下降的度数
(公顷)与当地气温下降的度数 (
( )之间有如下的对应数据:
)之间有如下的对应数据: (公顷) (公顷) | 20 | 40 | 50 | 60 | 80 |
 ( ( ) ) | 3 | 4 | 4 | 4 | 5 |
 关于
关于 的线性回归方程
的线性回归方程 ;
; ?
? .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 呈线性相关关系,回归方程为
呈线性相关关系,回归方程为 ,则变量
,则变量 是( )
是( ) | A.线性正相关关系 | B.由回归方程无法判断其正负相关 |
| C.线性负相关关系 | D.不存在线性相关关系 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 位女同学,
位女同学, 位男同学中随机抽取一个容量为
位男同学中随机抽取一个容量为 的样本进行分析。
的样本进行分析。 位同学,数学成绩由低到高依次为:
位同学,数学成绩由低到高依次为: ;
; ,若规定
,若规定 分(含
分(含 分)以
分)以 上为优秀,记
上为优秀,记 为这
为这 位同学中数学和物理分数均为优秀的人数,求
位同学中数学和物理分数均为优秀的人数,求 的分布列和数学期望;
的分布列和数学期望; 位同学的数学、物理分数事实上对应下表:
位同学的数学、物理分数事实上对应下表:| 学生编号 |  |  |  |  |  |  |  |  |
数学分数 |  |  |  |  |  |  |  |  |
物理分数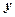 |  |  |  |  |  |  |  |  |
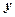 与
与
 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出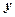 与
与 的线性回归方程(系数精确到
的线性回归方程(系数精确到 ).(参考公式:
).(参考公式: ,其中
,其中 ,
, ; 参考数据:
; 参考数据: ,
, ,
,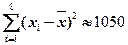 ,
, ,
,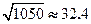 ,
, ,
, )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题


 线性相关系数为
线性相关系数为 线性相关系数为
线性相关系数为 线性相关系数为
线性相关系数为
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com