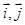是两个不共线向量.已知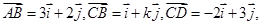若三点共线.则实数的值为题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

是两个不共线向量，已知若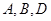三点共线，则实数的值为

5；

解析试题分析：因为所以
因为三点共线，所以3×（3-k）－2×(-3）=0,k=5.
考点：本题主要考查向量的线性运算，共线点的确定方法。
点评：证明三点共线的方法是，先证明相关向量共线。三点共线，则相关向量共线，对应坐标成比例。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

(1)由“若ab=ac(a≠0，a，b，c∈R)，则b=c”；类比“若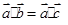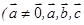（为三个向量），则”；
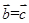（2）如果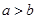，那么；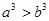
（3）若回归直线方程为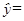1.5x+45，x∈{1,5,7,13,19}，则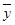=58.5；
（4）当n为正整数时，函数N（n）表示n的最大奇因数，如N（3）=3，N（10）=5，，由此可得函数N（n）具有性质：当n为正整数时，N（2n）= N（n），N（2n-1）=2n-1．
上述四个推理中，得出结论正确的是（写出所有正确结论的序号）.