【题目】已知函数
．
（1）当
时，求函数
的极值；
（2）当
时，若不等式
恒成立，求实数
的取值范围．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某外卖平台为提高外卖配送效率，针对外卖配送业务提出了两种新的配送方案，为比较两种配送方案的效率，共选取50名外卖骑手，并将他们随机分成两组，每组25人，第一组骑手用甲配送方案，第二组骑手用乙配送方案.根据骑手在相同时间内完成配送订单的数量（单位：单）绘制了如下茎叶图：
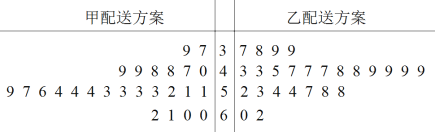
（1）根据茎叶图，求各组内25位骑手完成订单数的中位数，已知用甲配送方案的25位骑手完成订单数的平均数为52，结合中位数与平均数判断哪种配送方案的效率更高，并说明理由；
（2）设所有50名骑手在相同时间内完成订单数的平均数
，将完成订单数超过记为“优秀”，不超过记为“一般”，然后将骑手的对应人数填入下面列联表；
优秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
（3）根据（2）中的列联表，判断能否有
的把握认为两种配送方案的效率有差异.
附：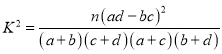
，其中
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】FEV1（一秒用力呼气容积）是肺功能的一个重要指标.为了研究某地区10～15岁男孩群体的FEV1与身高的关系，现从该地区A、B、C三个社区10～15岁男孩中随机抽取600名进行FEV1与身高数据的相关分析.
（1）若A、B、C三个社区10～15岁男孩人数比例为1：3：2，按分层抽样进行抽取，请求出三个社区应抽取的男孩人数.
（2）经过数据处理后，得到该地区10～15岁男孩身高
(cm)与FEV1
(L)对应的10组数据
，并作出如下散点图：
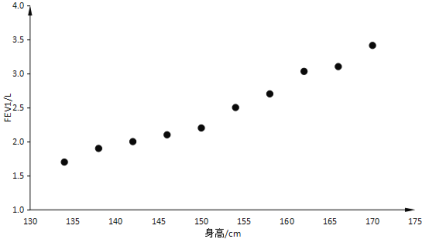
经计算得：
，
，
，
，的相关系数
.
①请你利用所给公式与数据建立关于的线性回归方程，并估计身高160cm的男孩的FEV1的预报值
.
②已知若①中回归模型误差的标准差为
，则该地区身高160cm的男孩的FEV1的实际值落在
，
内的概率为
.现已求得
，若该地区有两个身高160cm的12岁男孩M和N，分别测得FEV1值为2.8L和2.3L，请结合概率统计知识对两个男孩的FEV1指标作出一个合理的推断与建议.
附：样本
的相关系数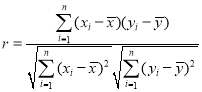
，其回归方程
的斜率和截距的最小二乘法估计分别为
，
，
．
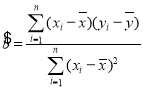查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】直角坐标系
中，圆
（
为参数）上的每一点的横坐标不变，纵坐标变为原来的
，得到曲线
．以坐标原点
为极点，
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
．
（1）求的普通方程和的直角坐标方程；
（2）设与两坐标轴分别相交于
两点，点
在上，求
的面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
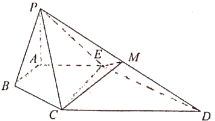
【题目】如图所示的几何体
中，
和
均为以
为直角顶点的等腰直角三角形，
，
，
，
，
为
的中点.
（1）求证：
；
（2）求二面角
的大小；
（3）设
为线段
上的动点，使得平面
平面
，求线段
的长.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
是公差不为零的等差数列，满足
，
，设正项数列
的前
项和为
，且
．
（1）求数列和的通项公式；
（2）在
和
之间插入1个数
，使、、成等差数列；在和
之间插入2个数
、
，使、、、成等差数列；
；在
和
之间插入个数
、
、、
，使、、、、、成等差数列．
① 求
；
② 对于①中的
，是否存在正整数
、，使得
成立？若存在，求出所有的正整数对
；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点为
，若△
的三个顶点都在抛物线
上，且
，则称该三角形为“核心三角形”.
（1）是否存在“核心三角形”，其中两个顶点的坐标分别为
和
？请说明理由；
（2）设“核心三角形”的一边
所在直线的斜率为4，求直线的方程；
（3）已知△是“核心三角形”，证明：点
的横坐标小于2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
