
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() ,
,![]() ,设正项数列
,设正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)在![]() 和
和![]() 之间插入1个数
之间插入1个数![]() ,使
,使![]() 、
、![]() 、
、![]() 成等差数列;在
成等差数列;在![]() 和
和![]() 之间插入2个数
之间插入2个数![]() 、
、![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 成等差数列;
成等差数列;![]() ;在
;在![]() 和
和![]() 之间插入
之间插入![]() 个数
个数![]() 、
、![]() 、
、![]() 、
、![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 成等差数列.
成等差数列.
① 求![]() ;
;
② 对于①中的![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() 成立?若存在,求出所有的正整数对
成立?若存在,求出所有的正整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②存在符合题意的正整数对
;②存在符合题意的正整数对![]() ,它们为
,它们为![]() 和
和![]() .
.
【解析】
(1)求出等差数列的首项和公差即得数列![]() 的通项公式,由题得当
的通项公式,由题得当![]() 时,
时,![]() ,
,![]() ,相减即得
,相减即得![]() 的通项公式;
的通项公式;
(2)①![]() ,再利用错位相减法求和得解;②假设存在正整数
,再利用错位相减法求和得解;②假设存在正整数![]() ,使得
,使得![]() ,化简得
,化简得![]() ,令
,令![]() ,证明
,证明![]() 时,
时,![]() ,列举得解.
,列举得解.
(1)设数列![]() 的公差为
的公差为![]() ,则由
,则由![]() 可得
可得![]() ,
,
再由![]() 化简得:
化简得:![]() ,解得:
,解得:![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() 得:
得:![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,
,
两式相减得![]() ,∴
,∴![]() .
.
(2)①![]() ,
,
![]() ,
,
设![]() ,
,
所以![]() ,
,
上面两式错位相减得![]() ,
,
所以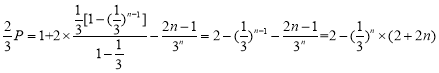
所以![]() ,
,
∴![]() .
.
②假设存在正整数![]() ,使得
,使得![]() ,
,
代入化简得![]() ,即
,即![]() ,
,
令![]() ,
,
则由![]() 可得:
可得:![]() .
.
当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ,舍去;
,舍去;
当![]() 时,
时,![]() ,舍去;
,舍去;
当![]() 时,
时,![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]() ,符合题意;
,符合题意;
综上:存在符合题意的正整数对![]() ,它们为
,它们为![]() 和
和![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() 、
、![]() (不与左右顶点重合),连结
(不与左右顶点重合),连结![]() 、
、![]() ,已知
,已知![]() 周长为8.
周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率为1,求
的斜率为1,求![]() 的面积;
的面积;
(3)设![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价![]() (单位:元/件)及相应月销量
(单位:元/件)及相应月销量![]() (单位:万件),对近5个月的月销售单价
(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下表数据:
的数据进行了统计,得到如下表数据:
月销售单价 | 9 |
| 10 |
| 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)该公司开展促销活动,当该产品月销售单价为7元/件时,其月销售量达到18万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() 万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
(Ⅲ)根据(Ⅰ)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中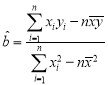 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信运动,是由腾讯开发的一个类似计步数据库的公众账号.用户可以通过关注微信运动公众号查看自己每天或每月行走的步数,同时也可以和其他用户进行运动量的![]() 或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
或点赞.加入微信运动后,为了让自己的步数能领先于朋友,人们运动的积极性明显增强,下面是某人2018年1月至2018年11月期间每月跑步的平均里程(单位:十公里)的数据,绘制了下面的折线图.
根据折线图,下列结论正确的是( )
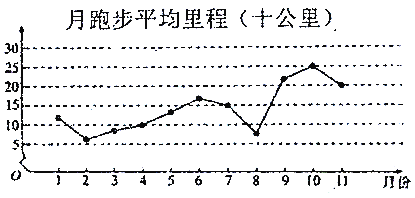
A. 月跑步平均里程的中位数为![]() 月份对应的里程数
月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在![]() 、
、![]() 月
月
D. ![]() 月至
月至![]() 月的月跑步平均里程相对于
月的月跑步平均里程相对于![]() 月至
月至![]() 月,波动性更小,变化比较平稳
月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人们通常以分贝(符号是![]() )为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为
)为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为![]() 的声音对应的等级为
的声音对应的等级为![]() ,则有
,则有![]() ,则
,则![]() 的声音与
的声音与![]() 的声音强度之比为( )
的声音强度之比为( )
A.10B.100C.1000D.10000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的普通方程为
的普通方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以坐标
.以坐标![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,建立极坐标系.
轴非负半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,
,![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,
,![]() .当
.当![]() 为等腰直角三角形时,求直线
为等腰直角三角形时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com