
【题目】定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且
,且![]() ,当
,当![]() 时,
时,![]() .已知方程
.已知方程![]() 在区间
在区间![]() 上所有的实数根之和为
上所有的实数根之和为![]() .将函数
.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,则
的图象,则![]() __________,
__________,![]() __________.
__________.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
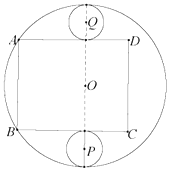
【题目】如图,是一块半径为4米的圆形铁皮,现打算利用这块铁皮做一个圆柱形油桶.具体做法是从![]() 中剪裁出两块全等的圆形铁皮
中剪裁出两块全等的圆形铁皮![]() 与
与![]() 做圆柱的底面,剪裁出一个矩形
做圆柱的底面,剪裁出一个矩形![]() 做圆柱的侧面(接缝忽略不计),
做圆柱的侧面(接缝忽略不计),![]() 为圆柱的一条母线,点
为圆柱的一条母线,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的一条直径上,
的一条直径上,![]() ,
,![]() 分别与直线
分别与直线![]() 、
、![]() 相切,都与
相切,都与![]() 内切.
内切.
(1)求圆形铁皮![]() 半径的取值范围;
半径的取值范围;
(2)请确定圆形铁皮![]() 与
与![]() 半径的值,使得油桶的体积最大.(不取近似值)
半径的值,使得油桶的体积最大.(不取近似值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在50个不同地区的零售价格全部介于13元与18元之间,将各地价格按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,……,第五组
,……,第五组![]() .如图是按上述分组方法得到的频率分布直方图.
.如图是按上述分组方法得到的频率分布直方图.
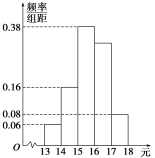
(1)求价格落在![]() 内的地区数;
内的地区数;
(2)借助频率分布直方图,估计该商品价格的中位数(精确到0.1);
(3)现从![]() ,
,![]() 这两组的全部样本数据中,随机选取两个地区的零售价格,记为
这两组的全部样本数据中,随机选取两个地区的零售价格,记为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产x万件,需另投入流动成本C(x)万元,当年产量小于7万件时,C(x)=![]() x2+2x(万元);当年产量不小于7万件时,C(x)=6x+1nx+
x2+2x(万元);当年产量不小于7万件时,C(x)=6x+1nx+![]() ﹣17(万元).已知每件产品售价为6元,假若该同学生产的产M当年全部售完.
﹣17(万元).已知每件产品售价为6元,假若该同学生产的产M当年全部售完.
(1)写出年利润P(x)(万元)关于年产量x(万件)的函数解析式;(注:年利润=年销售收人﹣固定成本﹣流动成本
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?(取e3≈20)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块三棱锥形木块![]() ,各面均是锐角三角形,其中面
,各面均是锐角三角形,其中面![]() 内有一点
内有一点![]() .
.
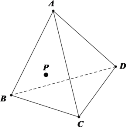
(1)若要在面![]() 内过点
内过点![]() 画一条线段
画一条线段![]() ,其中点
,其中点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() 与
与![]() 垂直,该如何求作?请在图中画出线段
垂直,该如何求作?请在图中画出线段![]() 并说明画法,不必证明;
并说明画法,不必证明;
(2)经测量,![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() 恰为三角形
恰为三角形![]() 的重心,
的重心,![]() 为(1)中所求线段,求三棱锥
为(1)中所求线段,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com