练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】给定空间中十个点，其中任意四点不在一个平面上，将某些点之间用线段相连，若得到的图形中没有三角形也没有空间四边形，试确定所连线段数目的最大值.

    【答案】15

    【解析】

    以这十个点为顶点、所连线段为边得一个十阶简单图G.

    下面证明：图G的边数不超过15.

    设图G的顶点为，共有k条边，用表示顶点的度.

    若对均成立，则.

    假设存在顶点满足.不妨设，且与均相邻.于是，之间没有边，否则，就形成三角形.从而，之间恰有n条边.

    对每个，至多与中的一个顶点相邻（否则，设与 相邻，则就对应了一个空间四边形的四个顶点，这与题设条件矛盾）.从而，与之间的边数至多为

    .

    在这个顶点之间，由于没有三角形，由托兰定理，知至多有条边.因此，图G的边数为

    .

    如图所示给出的图共有15条边，且满足要求.

    综上，所求边数的最大值为15.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知三棱柱的侧棱垂直于底面，，，点，分别为和的中点.

    （1）若，求三棱柱的体积；

    （2）证明：平面；

    （3）请问当为何值时，平面，试证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知直线l过点.

    （1）若直线l的纵截距和横截距相等，求直线l的方程；

    （2）若直线l与两坐标轴围成的三角形的面积为，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面是正方形， ，点E在棱PB上.

    （Ⅰ）求证：平面；

    （Ⅱ）当且E为PB的中点时，求AE与平面PDB所成的角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】①若直线与曲线有且只有一个公共点，则直线一定是曲线的切线；

    ②若直线与曲线相切于点，且直线与曲线除点外再没有其他的公共点，则在点附近，直线不可能穿过曲线；

    ③若不存在，则曲线在点处就没有切线；

    ④若曲线在点处有切线，则必存在.

    则以上论断正确的个数是（ ）

    A.0个B.1个C.2个D.3个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中， ， .

    （1）证明：平面平面；

    （2）若，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为有效预防新冠肺炎对老年人的侵害，某医院到社区检查老年人的体质健康情况．从该社区全体老年人中，随机抽取12名进行体质健康测试，根据测试成绩（百分制）绘制茎叶图如下．根据老年人体质健康标准，可知成绩不低于80分为优良，且体质优良的老年人感染新冠肺炎的可能性较低．

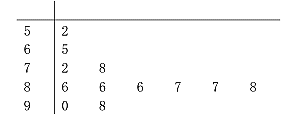
    （Ⅰ）从抽取的12人中随机选取3人，记表示成绩优良的人数，求的分布列及数学期望；

    （Ⅱ）将频率视为概率，根据用样本估计总体的思想，在该社区全体老年人中依次抽取10人，若抽到人的成绩是优良的可能性最大，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，x R其中a>0.

    （Ⅰ）求函数f(x)的单调区间；

    （Ⅱ）若函数f(x)在区间(-3,0)内恰有两个零点，求a的取值范围；

    （Ⅲ）当a=1时，设函数f(x)在区间[t,t+3]上的最大值为M(t)，最小值为m(t),记 ,求函数g(t)在区间[-4,-1]上的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为奇函数.

    （1）求实数的值；

    （2）用定义法讨论并证明函数的单调性.

    查看答案和解析>>

    同步练习册答案