
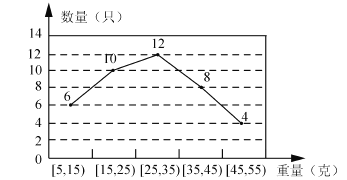
����Ŀ��ij�����̴����һˮֳ������һ��С��Ϻ���������ȡ40ֻ����ͳ�ƣ�����������ͳ�ƽ������ͼ��
��1�����¼�![]() Ϊ����������С��Ϻ����ȡһֻ������������35
Ϊ����������С��Ϻ����ȡһֻ������������35![]() ��С��Ϻ������
��С��Ϻ������![]() �Ĺ���ֵ��
�Ĺ���ֵ��
��2���Թ�������С��Ϻ��ƽ��������
��3��Ϊ��Ӧ�г������ƶ��������ԣ��þ������ֽ�����С��Ϻ�ֳ������ȼ������ƶ������۵��ۣ����±���
�ȼ� | һ��Ʒ | ����Ʒ | ����Ʒ |
������ |
|
|
|
���ۣ�Ԫ/ֻ�� | 1.2 | 1.5 | 1.8 |
�Թ���þ�������ÿǧ���������Ԫ��ȡ�������չ�����С��Ϻ�����ܻ������
���𰸡���1��![]() ��2��
��2��![]() ��3������С��Ϻÿǧ������
��3������С��Ϻÿǧ������![]() Ԫ
Ԫ
�������������������1������ͳ��ͼ�õ�����������![]() ��С��Ϻ��
��С��Ϻ��![]() �����������Ӧ�ĸ��ʣ�
�����������Ӧ�ĸ��ʣ�
��2����ͳ��ͼ�е����ݣ�����ƽ�����ļ��㹫ʽ�������������С��Ϻ��ƽ��������
��3�������������ɣ�2��֪��С��Ϻ��һ��Ʒ������Ʒ������Ʒ���������г���ϵʽ������ �ó�����.
�����������1������![]() ֻС��Ϻ������������
ֻС��Ϻ������������![]() ��С��Ϻ��
��С��Ϻ��![]() ��ֻ��
��ֻ��
����![]()
��2����ͳ��ͼ�п��Թ�������С��Ϻ��ƽ������Ϊ
![]()
![]() ���ˣ�
���ˣ�
��3����þ������չ�����С��Ϻÿǧ������![]() Ԫ.�����������ɣ�2��֪����
Ԫ.�����������ɣ�2��֪����![]() ֻС��Ϻ��һ��Ʒ������Ʒ������Ʒ����
ֻС��Ϻ��һ��Ʒ������Ʒ������Ʒ����![]() ֻ��
ֻ��![]() ֻ��
ֻ��![]() ֻ��Լ��
ֻ��Լ��![]()
����![]() ����
����![]()
�ʿ��Թ��Ƹþ������չ�����С��Ϻÿǧ������![]() Ԫ
Ԫ


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ�![]() ��ij�ۿڽ�һЩ��Ʒ�͵������е��ִ�
��ij�ۿڽ�һЩ��Ʒ�͵������е��ִ�![]() �ϣ����ִ�
�ϣ����ִ�![]() ����ʱ���ִ�
����ʱ���ִ�![]() λ�ڸۿ�
λ�ڸۿ�![]() ��ƫ��
��ƫ��![]() ����
����![]() ���20�����
���20�����![]() ����������30����ĺ�������������������ʻ�������ִ�
����������30����ĺ�������������������ʻ�������ִ�![]() ��ֱ�߷�����
��ֱ�߷�����![]() ����/Сʱ�ĺ���������ʻ������
����/Сʱ�ĺ���������ʻ������![]() Сʱ���ִ�
Сʱ���ִ�![]() ����.
����.
��1����ʹ����ʱ�ִ�![]() ������̣����ִ�
������̣����ִ�![]() �ĺ����ٶȴ�СӦΪ���٣�
�ĺ����ٶȴ�СӦΪ���٣�
��2�������ִ�![]() ����ߺ���ֻ�ܴﵽ30����/Сʱ�����ִ�
����ߺ���ֻ�ܴﵽ30����/Сʱ�����ִ�![]() �Զ���ٶȼ�ʲô���з�����������ʱ�����ִ�
�Զ���ٶȼ�ʲô���з�����������ʱ�����ִ�![]() ��������˵������.
��������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��Բ
��Բ![]()
��1����ֱ��![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() ������ͬ�㣬��
������ͬ�㣬��![]() ����Сֵ��
����Сֵ��
��2��ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() �����㾭����
�����㾭����![]() �������Ի��ഹֱ��ֱ��
�������Ի��ഹֱ��ֱ��![]() ��
��![]() �����Ƿֱ���Բ
�����Ƿֱ���Բ![]() ��Բ
��Բ![]() �ཻ������ֱ��
�ཻ������ֱ��![]() ��Բ
��Բ![]() ���صõ��ҳ�����ֱ��
���صõ��ҳ�����ֱ��![]() ��Բ
��Բ![]() ���صõ��ҳ��������ڣ������
���صõ��ҳ��������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������M={x|��2��x��2��N=y|0��y��2}�����������ĸ�ͼ�Σ������ܱ�ʾ��MΪ������NΪֵ��ĺ�����ϵ�� �� 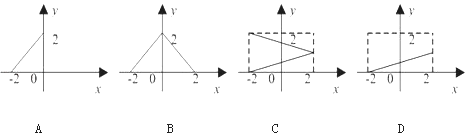
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ϊ�˽�Լ�����õ磬�ƻ��ڱ������о��������õ綨���������ȷ��һ���������õ�����![]() ���õ���������
���õ���������![]() �IJ��ְ�ƽ���շѣ�����
�IJ��ְ�ƽ���շѣ�����![]() �IJ��ְ�����շѣ�Ϊ�ˣ�����������100���������ƽ���õ�������λ���ȣ�����
�IJ��ְ�����շѣ�Ϊ�ˣ�����������100���������ƽ���õ�������λ���ȣ�����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �����Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
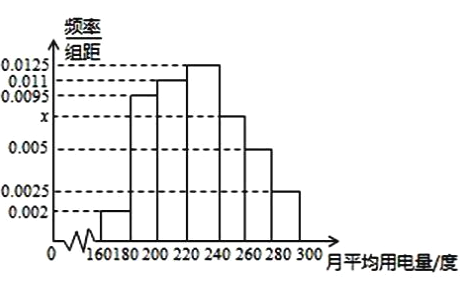
��1����ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2������ƽ���õ�������������λ����
��3�������������ϣ��ʹ![]() ���ҵľ���ÿ�µ��õ������������������������������˼�룬����Ϊ���õ�����
���ҵľ���ÿ�µ��õ������������������������������˼�룬����Ϊ���õ�����![]() Ӧ�ö�Ϊ���ٺ�����
Ӧ�ö�Ϊ���ٺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=f��x����R��Ϊ�溯������x��0ʱ��f��x��=3x2��9����f����2��=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������ס�������������Ʒ��ÿ����������ֱ�Ϊ3��Ԫ��2��Ԫ���ס��Ҳ�Ʒ����Ҫ��![]() �����豸�ϼӹ�����ÿ̨
�����豸�ϼӹ�����ÿ̨![]() �ϼӹ�1�������蹤ʱ�ֱ���1
�ϼӹ�1�������蹤ʱ�ֱ���1![]() ��2
��2![]() ���ӹ�1�������蹤ʱ�ֱ�Ϊ2
���ӹ�1�������蹤ʱ�ֱ�Ϊ2![]() ��1
��1![]() ��
�� ![]() �����豸ÿ����Чʹ��̨ʱ���ֱ�Ϊ400
�����豸ÿ����Чʹ��̨ʱ���ֱ�Ϊ400![]() ��500
��500![]() ����ΰ���������ʹ�������
����ΰ���������ʹ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���׳������������������۾���õ������й��������۵�ͳ�ƹ��ɣ�ÿ������Ʒx����̨�������ܳɱ�ΪG��x������Ԫ�������й̶��ɱ�Ϊ2.8��Ԫ������ÿ����1��̨�������ɱ�Ϊ1��Ԫ���ܳɱ�=�̶��ɱ�+�����ɱ�������������R��x������Ԫ������R��x��= ![]() ���ٶ��ò�Ʒ����ƽ�⣨�������IJ�Ʒ��������������������ͳ�ƹ��ɣ�������������⣺
���ٶ��ò�Ʒ����ƽ�⣨�������IJ�Ʒ��������������������ͳ�ƹ��ɣ�������������⣺
��1��д��������y=f��x���Ľ���ʽ������=�������멁�ܳɱ�����
��2��Ҫʹ�׳���ӯ���������x�ķ�Χ��
��3���׳���������̨��Ʒʱ����ʹӯ����ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��������ABC-A1B1Cl�У�M��N�ֱ�ΪCC1��A1B1���е㣮CA��CB1��CA=CB1��BA=BC=BB1.
(I)��֤��ֱ��MN//ƽ��CAB1��
(II)��֤��ֱ��BA1��ƽ��CAB1��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com