Question

6．抛物线y=x²上有一点A的横坐标为a，其中a∈（0，1），过点A的抛物线的切线l交x轴及直线x=1于B，C两点，直线x=1交x轴于D点．
（1）求直线l的方程；
（2）求△BCD的面积S（a），并求出a为何值时S（a）有最大值．

Answer 1

分析 （1）利用导数的运算法则可得y′，利用导数的几何意义即可得到切线的斜率，进而得到切线的方程；
（2）利用切线的方程即可得出点B，C的坐标，再利用三角形的面积公式，求得S（a），再由导数求得单调区间和最值，即可得出结论．

解答 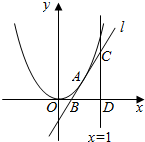解：（1）∵y=x²，∴y'=2x，
可得切线l的斜率为2a，
∴切线l的方程是y-a²=2a（x-a），即2ax-y-a²=0；
（2）由2ax-y-a²=0，令y=0，
解得x=$\frac{a}{2}$，∴B（$\frac{a}{2}$，0）；
令x=1，解得y=2a-a²，即C（1，2a-a²），
∴|BD|=1-$\frac{a}{2}$，|CD|=2a-a²，
∴△BCD的面积S（a）=$\frac{1}{2}$（1-$\frac{a}{2}$）（2a-a²）=$\frac{1}{4}$（a³-4a²+4a），
S′（a）=$\frac{1}{4}$（3a²-8a+4）=$\frac{1}{4}$（3a-2）（a-2），
令S'（a）=0，∵a∈（0，1），∴a=$\frac{2}{3}$．
当0＜a＜$\frac{2}{3}$时，S'（a）＞0；
当$\frac{2}{3}$＜a＜1时，S'（a）＜0．
∴a=$\frac{2}{3}$时，S（a）有最大值．

点评 熟练掌握利用导数研究函数的单调性、极值与最值，导数的几何意义等是解题的关键．