
长度为![]() (
(![]() >0)的线段AB的两个端点A、B分别在
>0)的线段AB的两个端点A、B分别在![]() 轴和y轴上滑动,点P在线段AB上,且满足
轴和y轴上滑动,点P在线段AB上,且满足![]() (A为常数,且
(A为常数,且![]() ).
).
(1)求点P的轨迹方程C;
(2)当![]() 时,过点M(1,0)作两条互相垂直的直线
时,过点M(1,0)作两条互相垂直的直线![]() 和
和![]() ,
,![]() 和
和![]() 分别与曲线C相交于点N和Q(N、Q都异于点M),试问△MNQ能不能是等腰三角形?若能,请说明这样的三角形有几个;若不能,请说明理由.
分别与曲线C相交于点N和Q(N、Q都异于点M),试问△MNQ能不能是等腰三角形?若能,请说明这样的三角形有几个;若不能,请说明理由.
解:(1)依题意,设点A、B的坐标分别为(![]() ,0)、(0,
,0)、(0,![]() ),点P的坐标为(
),点P的坐标为(![]() ).
).
由![]() ,得
,得![]() )
)
=(![]() ).
).
∴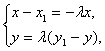 即
即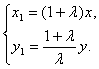
∵|AB|=![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴点P的轨迹方程C是![]() .
.
(2)当![]() 时,曲线C的方程是
时,曲线C的方程是![]() ,故点M(1,0)在曲线C上.
,故点M(1,0)在曲线C上.
依题意,可知直线![]() 和
和![]() 都不可能与坐标轴平行,可设直线
都不可能与坐标轴平行,可设直线![]() 方程为
方程为![]() ,
,
直线![]() 方程为
方程为![]() ,不妨设
,不妨设![]() .
.
由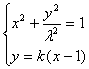 消去y得
消去y得
![]() .
.
由![]() ,又
,又![]() ,得
,得![]() ,
,
∴![]()
=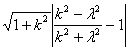
=![]() .
.
同理可得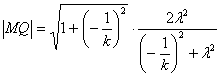
=![]() .
.
假设△MNQ是等腰三角形,则|MN|=|MQ|,
即![]() ,
,
化简得![]() ,
,
∴![]() 或
或![]() ①
①
①式的判别式△=![]() ,
,
若△=![]() ,解得
,解得![]() ,此时①式无解;
,此时①式无解;
若△=![]() =0,解得
=0,解得![]() ,由①式得
,由①式得![]() =1;
=1;
若△=![]() >0,解得
>0,解得![]() ,由①式得
,由①式得![]()
(可以验证![]() ≠1且
≠1且![]() >0).
>0).
综上所述,△MNQ可以是等腰三角形,当0<![]() ≤
≤![]() 时,这样的三角形有一个;
时,这样的三角形有一个;
当![]() 时,这样的三角形有三个.
时,这样的三角形有三个.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
(2010湖北理数)15.设a>0,b>0,称![]() 为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
为a,b的调和平均数。如图,C为线段AB上的点,且AC=a,CB=b,O为AB中点,以AB为直径做半圆。过点C作AB的垂线交半圆于D。连结OD,AD,BD。过点C作OD的垂线,垂足为E。则图中线段OD的长度是a,b的算术平均数,线段 的长度是a,b的几何平均数,线段 的长度是a,b的调和平均数。
查看答案和解析>>
科目:高中数学 来源:2014届山西省高三9月月考文科数学试卷(解析版) 题型:选择题
已知函数f(x)=sin(ωx+ )(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象( )
)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象( )
A.向左平移 个单位长度
B.向右平移
个单位长度
B.向右平移 个单位长度
个单位长度
C.向左平移 个单位长度
D.向右平移
个单位长度
D.向右平移 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高二上学期期中考试数学试卷(解析版) 题型:填空题
已知两条直线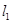 ::y=m 和
::y=m 和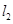 :y=
:y=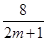 (m>0),直线
(m>0),直线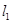 与函数
与函数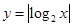 的图像从左至右相交于点A,B , 直线
的图像从左至右相交于点A,B , 直线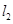 与函数
与函数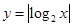 的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a 和b .当m 变化时,
的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a 和b .当m 变化时,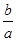 的最小值为
.
的最小值为
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省河西五市高三第二次联合考试理科数学试卷(解析版) 题型:选择题
若把函数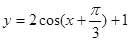 的图象向右平移
的图象向右平移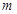 (
(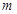 >0)个单位长度,使点
>0)个单位长度,使点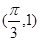 为其对称中心,则
为其对称中心,则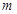 的最小值是
的最小值是
A.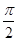 B.
B.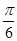 C.
C.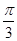 D.
D.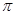
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com