
【题目】已知f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ;g(x)=1﹣x+
;g(x)=1﹣x+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣…﹣
﹣…﹣ ![]() ;设函数F(x)=[f(x+3)]2015[g(x﹣4)]2016 , 且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
;设函数F(x)=[f(x+3)]2015[g(x﹣4)]2016 , 且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
A.8
B.9
C.10
D.11
【答案】C
【解析】解:∵f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ,∴f′(x)=(1﹣x)+(x2﹣x3)+…+x2014
,∴f′(x)=(1﹣x)+(x2﹣x3)+…+x2014
=(1﹣x)(1+x2+x4+…+x2012)+x2014
当x=﹣1时,f′(x)=2×1007+1=2015>0,
当x≠﹣1时,f′(x)=(1﹣x)(1+x2+x4+…+x2012)+x2014
=(1﹣x) 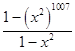 +x2014
+x2014
= ![]() >0,
>0,
∴f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() 在R上单调递增,
在R上单调递增,
∴f(0)=1>0,f(﹣1)=1﹣1﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣…﹣
﹣…﹣ ![]() <0,
<0,
∴函数f(x)在(﹣1,0)内有唯一零点,
由﹣1<x+3<0得:﹣4<x<﹣3,
∴f(x+3)在(﹣4,﹣3)上有唯一零点.
∴[f(x+3)]2015在(﹣4,﹣3)上有唯一零点,
∵g(x)=1﹣x+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣…﹣
﹣…﹣ ![]() ,
,
∴g′(x)=(﹣1+x)+(﹣x2+x3)+…﹣x2015
=﹣[(1﹣x)+(x2﹣x3)+…+x2015]
=﹣f′(x)<0,
∴g(x)在R上单调递减,
又g(1)=1﹣1 ![]() >0,
>0,
g(2)= ![]() <0,
<0,
当n≥2时, ![]() =
= ![]() <0,
<0,
∴g(2)<0.
∴g(x)在(1,2)上有唯一零点,
由1<x﹣4<2得:5<x<6,
∴g(x﹣4)在(5,6)上有唯一零点.
∴[g(x﹣4)]2016在(5,6)上有唯一零点.
∵F(x)=[f(x+3)]2015[g(x﹣4)]2016 ,
∴F(x)的零即为[f(x+3)]2015和[g(x﹣4)]2016的零点.
∴F(x)的零点区间为(﹣4,﹣3)∪(5,6).
又b,a∈Z,
∴(b﹣a)min=6﹣(﹣4)=10.
故选:C.


科目:高中数学 来源: 题型:
【题目】正方体ABCD﹣A1B1C1D1中,E,F分别为棱AB,CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线( )
A.有无数条
B.有2条
C.有1条
D.不存在
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:一个圆锥的底面半径为2,高为6,在其中有一个半径为x的内接圆柱. 
(1)试用x表示圆柱的体积;
(2)当x为何值时,圆柱的侧面积最大,最大值是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x),其中a>0且a≠1,设h(x)=f(x)﹣g(x)
(1)求函数h(x)的定义域,判断h(x)的奇偶性并说明理由
(2)解不等式h(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知一个椭圆的中心在原点,左焦点为 ![]() ,且过D(2,0).
,且过D(2,0).
(1)求该椭圆的标准方程;
(2)若P是椭圆上的动点,点A(1,0),求线段PA中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不过第二象限的直线l:ax﹣y﹣4=0与圆x2+(y﹣1)2=5相切.
(1)求直线l的方程;
(2)若直线l1过点(3,﹣1)且与直线l平行,直线l2与直线l1关于直线y=1对称,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(2x﹣1),g(x)=ax﹣a(a∈R).
(1)若y=g(x)为曲线y=f(x)的一条切线,求a的值;
(2)已知a<1,若存在唯一的整数x0 , 使得f(x0)<g(x0),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax,(e为自然对数的底数). (Ⅰ)讨论f(x)的单调性;
(Ⅱ)若对任意实数x恒有f(x)≥0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2ωx+2sinωxcosωx(ω>0)的最小正周期为π.
(1)求f( ![]() )的值;
)的值;
(2)求函数f(x)的单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com