
分析 (1)求出圆心与半径,写出圆的方程即可.
(2)通过题意解出OC的方程,解出t 的值,直线y=-2x+4与圆C交于点M,N,判断t是否符合要求,可得圆的方程.
解答 解:(1)a=2时,以点C(2,1)为圆心的圆与x轴相交于O,A两点,与y轴相交于O,B两点,
∵圆C过原点O,
∴OC2=22+12=5.
则圆C的方程是(x-2)2+(y-1)2=5,
(2)∵圆C过原点O,
∴OC2=a2+$\frac{4}{{a}^{2}}$,
则圆C的方程是(x-a)2+(y-$\frac{2}{a}$)2=a2+$\frac{4}{{a}^{2}}$,
令x=0,得y1=0,y2=$\frac{4}{a}$,
令y=0,得x1=0,x2=2a
∴S△OAB=$\frac{1}{2}$OA×OB=$\frac{1}{2}$×|$\frac{4}{a}$|×|2a|=4,
即:△OAB的面积为定值;
(3)∵|OM|=|ON|,|CM|=|CN|,
∴OC垂直平分线段MN,
∵kMN=-2,∴koc=$\frac{1}{2}$,
∴直线OC的方程是y=$\frac{1}{2}$x,
∴$\frac{2}{a}$=$\frac{1}{2}$t,解得:a=2或a=-2,
当a=-2时,圆心C的坐标为(-2,-1),OC=$\sqrt{5}$,
此时C到直线y=-2x+4的距离d=$\frac{9}{\sqrt{5}}$>$\sqrt{5}$,
圆C与直线y=-2x+4不相交,
∴a=-2不符合题意舍去,
∴圆C的方程为(x-2)2+(y-1)2=5.
当t=2时,圆心C的坐标为(2,1),OC=$\sqrt{5}$,
此时C到直线y=-2x+4的距离d=$\frac{1}{\sqrt{5}}$<$\sqrt{5}$,
圆C与直线y=-2x+4相交于两点,
|MN|=$2\sqrt{{r}^{2}-{d}^{2}}$=$2\sqrt{5-\frac{1}{5}}$=$\frac{4}{5}\sqrt{30}$.
点评 本题考查直线与圆的位置关系,圆的标准方程等有关知识,是中档题.


科目:高中数学 来源: 题型:解答题
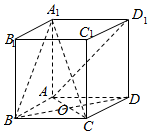 如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为2的菱形,且∠ABC=60°,AA1=3,AC,BD相交于点O,E为线段AD1上一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为2的菱形,且∠ABC=60°,AA1=3,AC,BD相交于点O,E为线段AD1上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
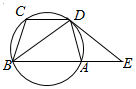 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 实轴长为$4\sqrt{2}$,虚轴长为2 | B. | 实轴长为$8\sqrt{2}$,虚轴长为4 | ||
| C. | 实轴长为2,虚轴长为$4\sqrt{2}$ | D. | 实轴长为4,虚轴长为$8\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com