
分析 将两个分式的1移项,然后通分,化为整式不等式解之.
解答 解:(1)$\frac{x-1}{2x}$≤1⇒$\frac{x-1}{2x}-1≤0$⇒$\frac{-x-1}{2x}≤0$⇒$\frac{x+1}{2x}≥0$⇒2x(x+1)≥0,且x≠0⇒x>0或x≤-1;
故$\frac{x-1}{2x}$≤1的解集为{x|x>0或x≤-1};
(2)$\frac{{x}^{2}-2x+2}{x}$>1⇒$\frac{{x}^{2}-3x+2}{x}>0$⇒(x-2)(x-1)x>0⇒x>2或0<x<1,
所以不等式的解集为{x|x>2或0<x<1}.
点评 本题考查了分式不等式的解法;注意:分式不等式在未明确分母符号的情况下,不能去分母.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
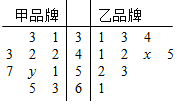 某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动,威调查这100天的日销售情况,用简单随机抽样抽取10天进行统计,以它们的销售数量(单位:件)作为样本,样本数据的茎叶图如图.已知该样本中,甲品牌牛奶销量的平均数为48件,乙品牌牛奶销量的中位数为43件,将日销量不低于50件的日期称为“畅销日”.
某商场对甲、乙两种品牌的牛奶进行为期100天的营销活动,威调查这100天的日销售情况,用简单随机抽样抽取10天进行统计,以它们的销售数量(单位:件)作为样本,样本数据的茎叶图如图.已知该样本中,甲品牌牛奶销量的平均数为48件,乙品牌牛奶销量的中位数为43件,将日销量不低于50件的日期称为“畅销日”.| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| 畅销日天数 | 非畅销日天数 | 合计 | |
| 甲品牌 | 50 | 50 | 100 |
| 乙品牌 | 30 | 70 | 100 |
| 合计 | 80 | 120 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
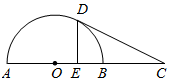 如图,AB是半圆O的直径,延长AB到C,使BC=$\sqrt{2}$,CD切半圆O于点D,DE⊥AB,垂足为E.若AE:EB=3:1,求DE的长.
如图,AB是半圆O的直径,延长AB到C,使BC=$\sqrt{2}$,CD切半圆O于点D,DE⊥AB,垂足为E.若AE:EB=3:1,求DE的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
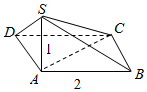 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,∠ADC=60°,SA=1,AB=2,SB=$\sqrt{5}$,平面SAB⊥底面ABCD,直线SC与底面ABCD所成的角为30°
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,∠ADC=60°,SA=1,AB=2,SB=$\sqrt{5}$,平面SAB⊥底面ABCD,直线SC与底面ABCD所成的角为30°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
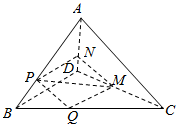 如图,在四面体ABCD中,截面PQMN是平行四边形,
如图,在四面体ABCD中,截面PQMN是平行四边形,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.6 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com