
定义域为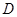 的函数
的函数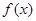 同时满足条件:①常数
同时满足条件:①常数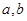 满足
满足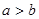 ,区间
,区间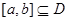 ,②使
,②使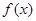 在
在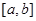 上的值域为
上的值域为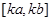
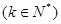 ,那么我们把
,那么我们把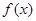 叫做
叫做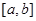 上的“
上的“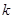 级矩形”函数.函数
级矩形”函数.函数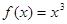 是
是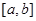 上的“1级矩形”函数,则满足条件的常数对
上的“1级矩形”函数,则满足条件的常数对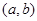 共有( )
共有( )
 1对
1对 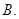 2对
2对
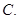 3对
3对  4对
4对
科目:高中数学 来源: 题型:
已知定义域为![]() 的函数
的函数![]() 同时满足以下三个条件:
同时满足以下三个条件:
[1] 对任意的![]() ,总有
,总有![]() ;
;
[2] ![]() ;
;
[3] 若![]() ,
,![]() ,且
,且![]() ,则有
,则有![]() 成立,
成立,
并且称![]() 为“友谊函数”,请解答下列各题:
为“友谊函数”,请解答下列各题:
(1)若已知![]() 为“友谊函数”,求
为“友谊函数”,求![]() 的值;
的值;
(2)函数![]() 在区间
在区间![]() 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知![]() 为“友谊函数”,假定存在
为“友谊函数”,假定存在![]() ,使得
,使得![]() 且
且![]() ,
,
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义域为![]() 的函数
的函数![]() 同时满足以下三个条件:
同时满足以下三个条件:
[1] 对任意的![]() ,总有
,总有![]() ;
;
[2] ![]() ;
;
[3] 若![]() ,
,![]() ,且
,且![]() ,则有
,则有![]() 成立,
成立,
并且称![]() 为“友谊函数”,请解答下列各题:
为“友谊函数”,请解答下列各题:
(1)若已知![]() 为“友谊函数”,求
为“友谊函数”,求![]() 的值;
的值;
(2)函数![]() 在区间
在区间![]() 上是否为“友谊函数”?并给出理由.
上是否为“友谊函数”?并给出理由.
(3)已知![]() 为“友谊函数”,假定存在
为“友谊函数”,假定存在![]() ,使得
,使得![]() 且
且![]() ,
,
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源:山东省潍坊市09-10学年高二下学期质量调研抽测数学试题 题型:解答题
(本小题满分12分)
已知定义域为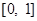 的函数同时满足以下三个条件:
的函数同时满足以下三个条件:
①对任意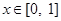 ,总有
,总有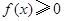 ;
;
②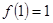 ;
;
③若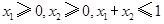 ,则有
,则有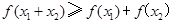 成立.
成立.
(I)求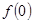 的值;
的值;
(II)判断函数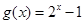 在区间
在区间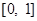 上是否同时适合①②③,并给出证明.
上是否同时适合①②③,并给出证明.
查看答案和解析>>
科目:高中数学 来源:云南省玉溪一中09-10学年高一上学期期中考试 题型:解答题
已知定义域为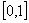 的函数同时满足以下三条:①对任意的
的函数同时满足以下三条:①对任意的
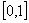 ,总有
,总有 ;②
;② ;③若
;③若
 则有
则有 成立.解答下列各题:
成立.解答下列各题:
(1)求 的值;
的值;
(2)函数 在区间
在区间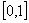 上是否同时适合①②③?并予以证明;
上是否同时适合①②③?并予以证明;
(3)假定存在
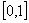 ,使得
,使得
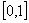 且
且 ,求证
,求证 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com