Question

（2012•顺河区一模）偶函数f(x)满足f(x-2)=f(x+2)，且在x∈[0，2]时，f(x)=2cos

π

4

x，则关于x的方程f(x)=(

1

2

)x，在x∈[-2，6]上解的个数是（　　）

A．l

B．2

C．3

D．4

Answer 1

分析：根据题意，函数f（x）是周期为4的是偶函数，在[0，2]上的表达式为f(x)=2cos

π

4

x，由此不难作出f（x）在[-2，6]上的图象，再在同一坐标系内作出函数y=（

1

2

）^x的图象，观察两个图象的交点个数，即得本题方程实数根的个数．

解答：解：∵当x∈[0，2]时，0≤

π

4

x≤

π

2

，f(x)=2cos

π

4

x
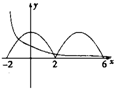
∴函数f（x）在x=0时，函数值有最大值f（0）=2cos0=2，
在x=2时，函数值有最小值f（2）=2cos

π

2

=0．
由此作出函数f（x）在x∈[0，2]时的图象，呈减函数趋势如图
∵函数f（x）是偶函数，
∴f（x）在[-2，0]上的图象与[0，2]上的图象关于y轴对称，如图所示
∵函数f（x）满足f（x-2）=f（x+2），∴函数f（x）是周期T=4的周期函数．
因此，将f（x）在[-2，2]上的图象向右平移一个周期，得f（x）在[2，6]上的图象
∴函数f（x）在[-2，6]上的图象如右图所示，是位于x轴上方的两段余弦型曲线弧
在同一坐标系内作出函数y=（

1

2

）^x的图象，可得它经过点（0，1），呈减函数趋势如图
因为两个图象有4个交点，得关于x的方程f（x）=（

1

2

）^x的实数根也有4个
故选D

点评：本题以一个关于x的方程根的个数讨论为载体，考查了函数的单调性与奇偶性、基本初等函数图象作法和函数的周期等知识点，属于中档题．