
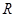 的函数
的函数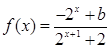 是奇函数.
是奇函数.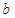 的值;
的值;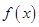 的单调性;
的单调性;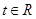 ,不等式
,不等式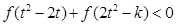 恒成立,求
恒成立,求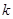 的取值范围.
的取值范围. 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:不详 题型:解答题
 年(
年( 为正整数,2012年为第一年)的利润为
为正整数,2012年为第一年)的利润为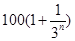 万元.设从2012年起的前
万元.设从2012年起的前 年,该厂不开发新项目的累计利润为
年,该厂不开发新项目的累计利润为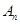 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).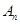 ,
, 的表达式;
的表达式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,曲线
,曲线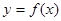 在点
在点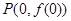 处的切线方程为
处的切线方程为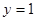
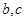 的值
的值 的三条不同切线,求
的三条不同切线,求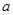 的取值范围
的取值范围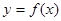 在点
在点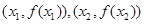 处的切线都过点(0,2),证明:当
处的切线都过点(0,2),证明:当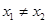 时,
时,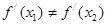
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
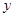 (万元)随投资收益
(万元)随投资收益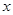 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%. 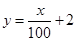 ;②
;②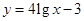 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

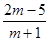 ,则实数m的取值集合是( )
,则实数m的取值集合是( )A.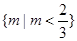 | B.{O,2} |
C.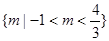 | D.{0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com