
如图,在直四棱柱![]() 中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2, AA
中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2, AA![]() =2, E、E
=2, E、E![]() 、F分别是棱AD、AA
、F分别是棱AD、AA![]() 、AB的中点。
、AB的中点。
(Ⅰ)证明:直线![]() ∥平面
∥平面![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅱ)求二面角![]() 的余弦值
的余弦值

(Ⅱ)![]()
解法一:(1)在直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,取A1B1的中点F1,
中,取A1B1的中点F1,
 连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E![]() 分别是棱AD、AA
分别是棱AD、AA![]() 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为![]() 平面FCC
平面FCC![]() ,
,![]() 平面FCC
平面FCC![]() ,
,
所以直线EE![]() //平面FCC
//平面FCC![]() .······6分
.······6分
(2)因为AB=4, BC=CD=2, 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC![]() -C的一个平面角, 在△BCF为正三角形中,
-C的一个平面角, 在△BCF为正三角形中,![]() ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵![]() ∴
∴![]() , w.w.w.k.s.5.u.c.o.m
, w.w.w.k.s.5.u.c.o.m ![]()
![]() ··········11分
··········11分

在Rt△OPF中,![]() ,
,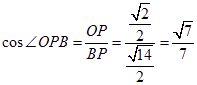 ,所以
,所以
二面角B-FC![]() -C的余弦值为
-C的余弦值为![]() .·······14分
.·······14分


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源:2012-2013学年山西省高三第八次模拟文科数学试卷(解析版) 题型:解答题
如图,在直四棱柱 中,已知
中,已知 ,
, .
.

(Ⅰ)求证: ;
;
(Ⅱ)设 是
是 上一点,试确定
上一点,试确定 的位置,使
的位置,使 平面
平面 ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省青岛市高三统一质量检测理科数学试卷 题型:解答题
如图,在直四棱柱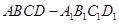 中,底面
中,底面 为平行四边形,且
为平行四边形,且
 ,
, ,
,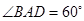 ,
, 为
为 的中点.
的中点.
(Ⅰ) 证明: ∥平面
∥平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三第四次月考数学文卷 题型:填空题
如图,在直四棱柱 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2,
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2,  =2,
E、
=2,
E、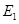 分别是棱AD、A
分别是棱AD、A 的中点.
的中点.

(1) 设F是棱AB的中点,证明:直线E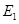 //平面FC
//平面FC ;
;
(2) 证明:平面D1AC⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源:2013届度江苏省江阴市高二第一学期期中数学试卷 题型:解答题
如图,在直四棱柱 中,已知
中,已知 ,
, .
.
(1)求证: ;
;
(2)设 是
是 上一点,试确定
上一点,试确定 的位置,使
的位置,使 平面
平面 ,并证明.
,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com