
分析:先考虑|x-1|+|y-a|=1的图象,图象是(0,a),(1,a-1),(1,a+1),(2,a)为端点的正方形,那么和O最远的应该是最远的两个端点之一,再对a进行分类讨论,如果a>0就是(1,a+1)或(2,a);如果a<0就是(1,a-1)或(2,a).再分类写出|
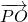
|平方的最大值.最后利用分段函数的图象,再读出|
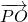
|
2取值范围为[

,17]时,a取值范围.
解答:
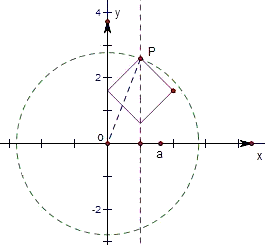
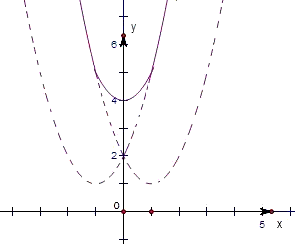
解:考虑|x-1|+|y-a|=1的图象,如图,
x必然是在0到2之间
x取到0或2那么y只能取a
x在两者之间y可以取两个值
x取到1则y可以取a+1或a-1,
图象是(0,a),(1,a-1),(1,a+1),(2,a)为端点的正方形,那么和O最远的应该是最远的两个端点之一,
如果a>0就是(1,a+1)或(2,a)
如果a<0就是(1,a-1)或(2,a)
这样一来,|
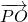
|平方的最大值就是:
当a>0,(a+1)
2+1 或 a
2+4
当a<0,(a-1)2+1 或 a
2+4
比较它们的大小:
当a≥1时,(a+1)
2+1;
-1<a<1时,a
2+4;
a≤-1时,(a-1)
2+1.
作以上函数图象,再读出y取值范围为[

,17]时
a取值范围是
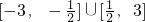
.
故答案为:
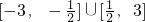
.
点评:本题主要考查了方程的曲线、向量的模及函数图象的应用,考查了数形结合思想、分类讨论思想.属于中档题.

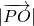 的最大值的取值范围为
的最大值的取值范围为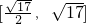 ,则实数a的取值范围是________.
,则实数a的取值范围是________.
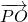 |平方的最大值.最后利用分段函数的图象,再读出|
|平方的最大值.最后利用分段函数的图象,再读出|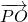 |2取值范围为[
|2取值范围为[ ,17]时,a取值范围.
,17]时,a取值范围. 解:考虑|x-1|+|y-a|=1的图象,如图,
解:考虑|x-1|+|y-a|=1的图象,如图,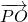 |平方的最大值就是:
|平方的最大值就是:
 ,17]时
,17]时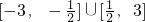 .
.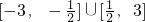 .
.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案