
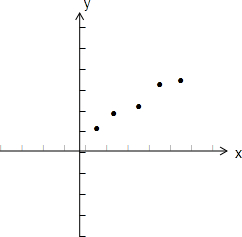
| x/万元 | 2 | 4 | 5 | 6 | 8 | 参考数据:
| |||||||||||||
| y/万件 | 30 | 40 | 60 | 50 | 70 |
| ? |
| b |
| |||||||
|
| |||||||
|
| ? |
| a |
. |
| y |
| ? |
| b |
. |
| x |
| |||||
|
. |
| x |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| y |
| 1 |
| n |
| n |
 |
| i=1 |
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
| ? |
| b |
| |||||||
|
| 1380-5×5×50 |
| 145-5×52 |
| ? |
| a |
. |
| y |
. |
| x |
| ? |
| y |
| (-0.5)2+3.52+102+(-6.5)2+0.52 |
| 202+102+102+02+202 |


科目:高中数学 来源: 题型:
| 1952 | 25 |
查看答案和解析>>
科目:高中数学 来源:同步题 题型:解答题
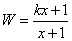 (x≥0),且知投入广告费1万元时,可销售2万件产品,预计此种产品的年销售收入等于年成本(万元)的150%与年广告费用的50%的和。
(x≥0),且知投入广告费1万元时,可销售2万件产品,预计此种产品的年销售收入等于年成本(万元)的150%与年广告费用的50%的和。查看答案和解析>>
科目:高中数学 来源: 题型:
(1)直接写出y与x之间的函数关系式;
(2)求第一年的年获利w与x之间的函数关系式,并说明投资的第一年,该公司是赢利还是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(![]() =1 521)
=1 521)
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省莆田一中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
 =1521)
=1521)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com