
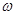 x+
x+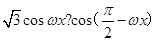 (
(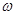 >0),且函数y=f(x)的图象相邻两条对称轴之间的距离为
>0),且函数y=f(x)的图象相邻两条对称轴之间的距离为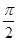 。
。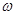 的值及f(x)的单调递增区间;
的值及f(x)的单调递增区间;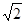 ,f(A)=1,求角C。(1)
,f(A)=1,求角C。(1) 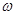 =1 增区间(kπ-
=1 增区间(kπ-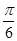 ,kπ+
,kπ+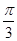 ),k
),k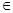 Z; (2)C=1050或150。
Z; (2)C=1050或150。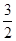 ,再根据A为三角形的内角,利用特殊角的三角函数值求出A的度数,然后由a,sinA与b的值,利用正弦定理求出sinB的值,由B为三角形的内角,且根据b小于a,利用三角形的边角关系得到B为锐角,利用特殊角的三角函数值求出B的度数,进而利用三角形的内角和定理求出C的度数.
,再根据A为三角形的内角,利用特殊角的三角函数值求出A的度数,然后由a,sinA与b的值,利用正弦定理求出sinB的值,由B为三角形的内角,且根据b小于a,利用三角形的边角关系得到B为锐角,利用特殊角的三角函数值求出B的度数,进而利用三角形的内角和定理求出C的度数.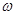 =1 增区间(kπ-
=1 增区间(kπ-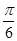 ,kπ+
,kπ+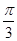 ),k
),k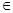 Z (6分)
Z (6分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:单选题
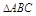 中,
中,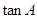 是以-4为第3项,4为第5项的等差数列的公差,
是以-4为第3项,4为第5项的等差数列的公差,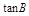 是以
是以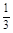 为第3项,9为第6项的等比数列的公比,则该三角形是
为第3项,9为第6项的等比数列的公比,则该三角形是| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.等腰三角形 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 与
与 成正比,与距离
成正比,与距离 的平方成反比,即
的平方成反比,即 ,设电灯可沿着BO移动,为了使水平面上的点A 处获得最大的亮度,则
,设电灯可沿着BO移动,为了使水平面上的点A 处获得最大的亮度,则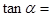 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com