
设无穷等比数列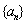 的公比为q,且
的公比为q,且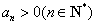 ,
,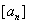 表示不超过实数
表示不超过实数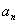 的最大整数(如
的最大整数(如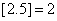 ),记
),记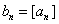 ,数列
,数列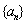 的前
的前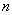 项和为
项和为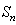 ,数列
,数列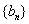 的前
的前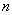 项和为
项和为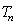 .
.
(Ⅰ)若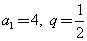 ,求
,求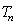 ;
;
(Ⅱ)若对于任意不超过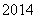 的正整数n,都有
的正整数n,都有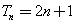 ,证明:
,证明: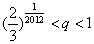 .
.
(Ⅲ)证明: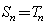 (
(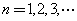 )的充分必要条件为
)的充分必要条件为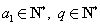 .
.
(Ⅰ)解:由等比数列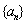 的
的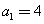 ,
,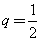 ,
,
得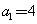 ,
,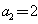 ,
,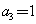 ,且当
,且当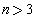 时,
时,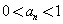 .
.
所以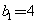 ,
,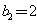 ,
,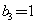 ,且当
,且当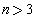 时,
时,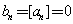 .
.
即 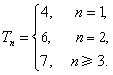
(Ⅱ)证明:因为 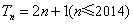 ,
,
所以 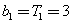 ,
,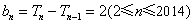 .
.
因为 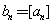 ,
,
所以 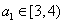 ,
,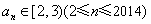 .
.
由 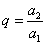 ,得
,得 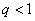 .
.
因为 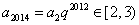 ,
,
所以 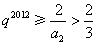 ,
,
所以 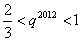 ,即
,即 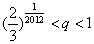 .
.
(Ⅲ)证明:(充分性)因为 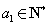 ,
,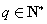 ,
,
所以 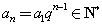 ,
,
所以 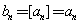 对一切正整数n都成立.
对一切正整数n都成立.
因为 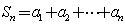 ,
,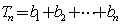 ,
,
所以 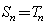 .
.
(必要性)因为对于任意的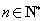 ,
,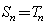 ,
,
当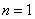 时,由
时,由 ,得
,得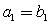 ;
;
当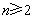 时,由
时,由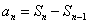 ,
,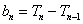 ,得
,得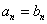 .
.
所以对一切正整数n都有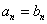 .
.
由 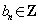 ,
,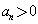 ,得对一切正整数n都有
,得对一切正整数n都有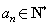 ,
,
所以公比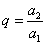 为正有理数.
为正有理数.
假设 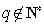 ,令
,令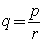 ,其中
,其中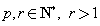 ,且
,且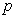 与
与 的最大公约数为1.
的最大公约数为1.
因为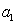 是一个有限整数,
是一个有限整数,
所以必然存在一个整数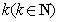 ,使得
,使得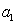 能被
能被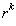 整除,而不能被
整除,而不能被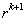 整除.
整除.
又因为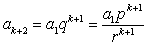 ,且
,且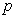 与
与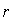 的最大公约数为1.
的最大公约数为1.
所以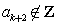 ,这与
,这与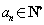 (
(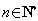 )矛盾.
)矛盾.
所以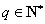 .
.
因此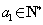 ,
,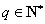 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
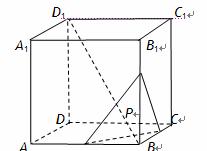
如图,正方体 的棱长为
的棱长为 ,动点P在对角线
,动点P在对角线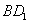 上,过点P作垂直于
上,过点P作垂直于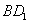 的平面
的平面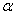 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设 x,则当
x,则当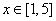 时,函数
时,函数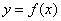 的值域为( )
的值域为( )
(A)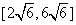 (B)
(B) (C)
(C) (D)
(D)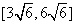
查看答案和解析>>
科目:高中数学 来源: 题型:
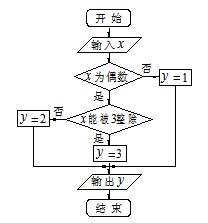
某算法的程序框图如图所示,其中输入的变量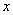 在
在 这
这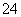 个整数中等可能随机产生.
个整数中等可能随机产生.
(Ⅰ)分别求出按程序框图正确编程运行时输出 的值为
的值为 的概率
的概率 ;
;
(Ⅱ)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行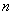 次后,统计记录了输出
次后,统计记录了输出 的值为
的值为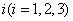 的频数.以下是甲、乙所作频数统计表的部分数据.
的频数.以下是甲、乙所作频数统计表的部分数据.
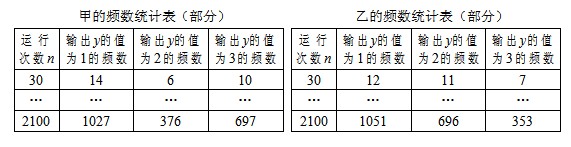
当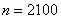 时,根据表中的数据,分别写出甲、乙所编程序各自输出
时,根据表中的数据,分别写出甲、乙所编程序各自输出 的值为
的值为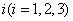 的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com