
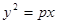 的焦点与椭圆
的焦点与椭圆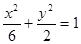 的右焦点重合,则p的值为
的右焦点重合,则p的值为

 ,
,
 B 4
B 4 C - 8 D 8
C - 8 D 8科目:高中数学 来源:不详 题型:解答题
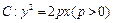 ,点
,点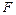 为其焦点,点
为其焦点,点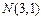 在抛物线
在抛物线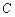 的内部,设点
的内部,设点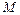 是抛物线
是抛物线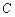 上的任意一点,
上的任意一点,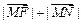 的最小值为4.
的最小值为4.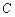 的方程;
的方程;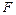 作直线
作直线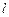 与抛物线
与抛物线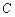 交于不同两点
交于不同两点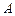 、
、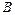 ,与
,与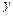 轴交于点
轴交于点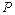 ,且
,且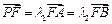 ,试判断
,试判断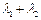 是否为定值?若是定值,求出该定值并证明;若不是定值,
是否为定值?若是定值,求出该定值并证明;若不是定值,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
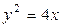 上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F
上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F A|=2,|FB|=5,
A|=2,|FB|=5,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
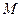 到定点
到定点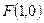 的距离与到定直线
的距离与到定直线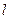 :
: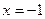 的距离相等,点C在直线
的距离相等,点C在直线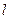 上。
上。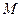 的轨迹方程。
的轨迹方程。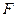 ,且法向量
,且法向量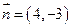 的直线与(1)中的轨迹相交于
的直线与(1)中的轨迹相交于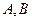 两点且点
两点且点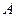 在
在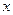 轴的上方。判断
轴的上方。判断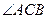 能否为钝角并说明理由。进一步研究
能否为钝角并说明理由。进一步研究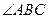 为钝角时点
为钝角时点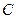 纵坐标的取值范围。
纵坐标的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
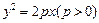 ,过定点
,过定点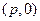 作两条互相垂直的直线
作两条互相垂直的直线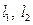 ,
,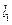 与抛物线交于
与抛物线交于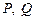 两点,
两点,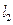 与抛物线交于
与抛物线交于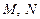 两点,设
两点,设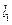 的斜率为
的斜率为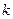 .若某同学已正确求得弦
.若某同学已正确求得弦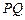 的中垂线在y轴上的截距为
的中垂线在y轴上的截距为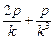 ,则弦MN的中垂线在y轴上的截距为
,则弦MN的中垂线在y轴上的截距为查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 直线l交抛物线
直线l交抛物线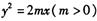 于A、B
于A、B 两点,若A,B两点满足
两点,若A,B两点满足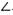 AQP=
AQP=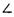 BQP,其中Q(-4,0),
BQP,其中Q(-4,0), 原点O为PQ的中点.
原点O为PQ的中点.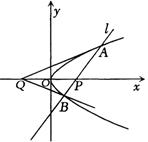
 ,使
,使 得
得 被以为直径的圆所截得的弦长为定值,如果存在,求出
被以为直径的圆所截得的弦长为定值,如果存在,求出 的方程,如果不存在,请说明理由
的方程,如果不存在,请说明理由查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com