
【题目】将下列问题的解答过程补充完整.
依次计算数列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前四项的值,由此猜测
,…的前四项的值,由此猜测![]() 的有限项的表达式,并用数学归纳法加以证明.
的有限项的表达式,并用数学归纳法加以证明.
解:计算 ![]() ,
,
![]() ,
,
![]() ① ,
① ,
![]() ② ,
② ,
由此猜想![]() ③ .(*)
③ .(*)
下面用数学归纳法证明这一猜想.
(i)当![]() 时,左边
时,左边![]() ,右边
,右边![]() ,所以等式成立.
,所以等式成立.
(ⅱ)假设当![]() 时,等式成立,即
时,等式成立,即
![]() ④ .
④ .
那么,当![]() 时,
时,
![]() ⑤
⑤
![]() ⑥
⑥
![]() ⑦ .
⑦ .
等式也成立.
根据(i)和(ⅱ)可以断定,(*)式对任何![]() 都成立.
都成立.
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面几何中的定理:△ABC中,若DE是△ABC的中位线,则有S△ADE∶S△ABC=1∶4;若三棱锥A-BCD有中截面EFG∥平面BCD,则截得三棱锥的体积与原三棱锥体积之间的关系式为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,
,![]() 分别是椭圆的左、右两焦点,过
分别是椭圆的左、右两焦点,过![]() 且倾斜角为
且倾斜角为![]() (
(![]() )的动直线
)的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点(如图所示,点
两点(如图所示,点![]() 在
在![]() 轴上方).当
轴上方).当![]() 时,弦
时,弦![]() 的长为
的长为![]() .
.

(1)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(2)若![]() 依次成等差数列,求直线
依次成等差数列,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为2的正方形ABCD沿PD、PC翻折至A、B两点重合,其中P是AB中点,在折成的三棱锥A(B)-PDC中,点Q在平面PDC内运动,且直线AQ与棱AP所成角为60,则点Q运动的轨迹是
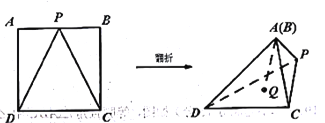
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com