
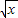 +1)=x+2
+1)=x+2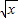 .
.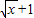 ,解出x和范围后代入函数解析式,然后把变量t换成x即可;也可以把等式的右边配方出现
,解出x和范围后代入函数解析式,然后把变量t换成x即可;也可以把等式的右边配方出现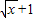 和常数的形式,从而求出函数f(x)的解析式;
和常数的形式,从而求出函数f(x)的解析式;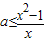 对任意的a∈[-1,1]恒成立,再把a当成变量列出关于x的不等式求解即可.
对任意的a∈[-1,1]恒成立,再把a当成变量列出关于x的不等式求解即可.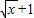 ,则t≥1,且x=(t-1)2,
,则t≥1,且x=(t-1)2,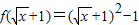 ,
,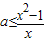 对任意的a∈[-1,1]恒成立,
对任意的a∈[-1,1]恒成立,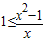 ,即x2-x-1≥0,
,即x2-x-1≥0,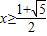 或
或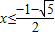 (舍去),
(舍去),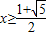 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| nf(n+1) |
| f(n) |
| 1 |
| s1 |
| 1 |
| s2 |
| 1 |
| sn |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f2(1)+f(2) |
| f(1) |
| f2(2)+f(4) |
| f(3) |
| f2(3)+f(6) |
| f(5) |
| f2(4)+f(8) |
| f(7) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com