
已知函数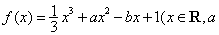 ,
,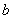 为实数)有极值,且在
为实数)有极值,且在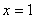 处的切线与直线
处的切线与直线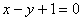 平行.
平行.
(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数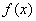 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(Ⅲ)设函数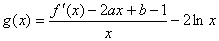 ,试判断函数
,试判断函数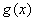 在
在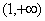 上的符号,
上的符号,
并证明: 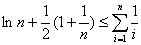
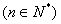 。
。
已知函数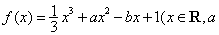 ,
,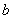 为实数)有极值,且在
为实数)有极值,且在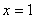 处的切线与直线
处的切线与直线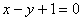 平行.
平行.
(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数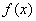 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(Ⅲ)设函数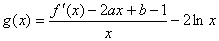 ,试判断函数
,试判断函数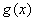 在
在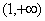 上的符号,
上的符号,
并证明: 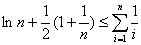
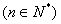 。
。
解:(Ⅰ)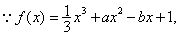
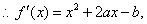 由题意
由题意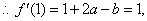
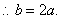
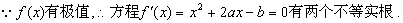
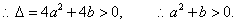 ②
②
由①、②可得,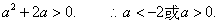
故实数a的取值范围是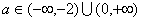
(Ⅱ)存在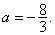
由(1)可知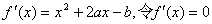 ,
,
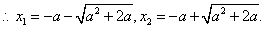 ,且
,且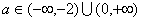
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| 单调增 | 极大值 | 单调减 | 极小值 | 单调增 |
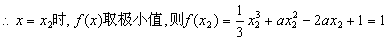 ,
,
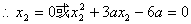
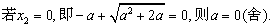
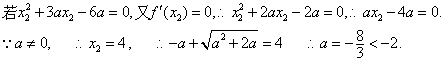
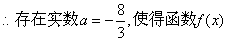 的极小值为1
的极小值为1
(Ⅲ)由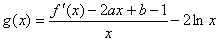
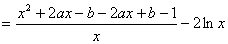
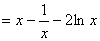
即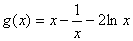
故,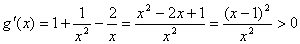
则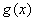 在
在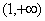 上是增函数,故
上是增函数,故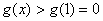 ,
,
所以,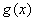 在
在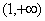 上恒为正。
上恒为正。
(注:只判断符号,未说明理由的,酌情给分)
当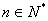 时,
时,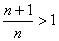 ,设
,设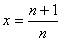 ,则
,则
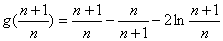
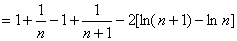
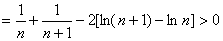
即,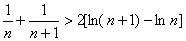
上式分别取 的值为1、2、3、……、
的值为1、2、3、……、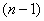 累加得:
累加得:

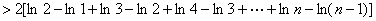 ,(
,(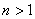 )
)
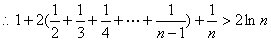 ,(
,(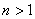 )
)
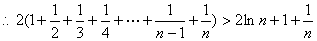 ,(
,(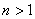 )
)
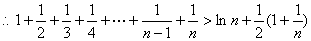 ,(
,(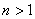 )
)
即,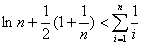 ,(
,(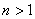 )
)
又当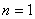 时,
时, ,
,
故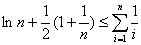 ,当且仅当
,当且仅当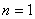 时取等号。1
时取等号。1


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
若一个2×2列联表中,由其数据计算得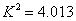 ,则有________把握认为这两个变量有关系
,则有________把握认为这两个变量有关系
参考数据:
|
| 0.050 | 0.010 | 0.001 |
| | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系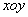 中,以
中,以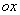 轴为始边,锐角
轴为始边,锐角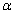 的终边与单位圆在第一象限交于点A,且点A的纵坐标为
的终边与单位圆在第一象限交于点A,且点A的纵坐标为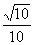 ,锐角
,锐角 的终边与射线x-7y=0(
的终边与射线x-7y=0(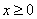 )重合.
)重合.
(1)求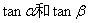 的值;(2) 求
的值;(2) 求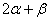 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下面给出了关于复数的三种类比推理:
①复数的乘法运算法则可以类比多项式的乘法运算法则;
②由向量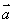 的性质
的性质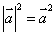 可以类比复数的性质
可以类比复数的性质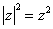 ;
;
③由向量加法的几何意义可以类比得到复数加法的几何意义。
A.①③ B.①② C.② D.③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com