
分析 由${({\sqrt{x}+\frac{2}{x^2}})^n}$展开式中只有第六项二项式系数最大,可得n=10.再利用$(\sqrt{x}+\frac{2}{{x}^{2}})^{10}$的通项公式即可得出.
解答 解:∵${({\sqrt{x}+\frac{2}{x^2}})^n}$展开式中只有第六项二项式系数最大,∴n=10.
∴$(\sqrt{x}+\frac{2}{{x}^{2}})^{10}$的通项公式:Tr+1=${∁}_{10}^{r}$$(\sqrt{x})^{10-r}(\frac{2}{{x}^{2}})^{r}$=2r${∁}_{10}^{r}$${x}^{5-\frac{5r}{2}}$,解得r=2.
∴常数项为:${2}^{2}{∁}_{10}^{2}$=180.
故答案为:10,180.
点评 本题参考二项式定理的展开式及其通项公式,考查了推理能力与计算能力,属于基础题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=x+\frac{4}{x}$ | B. | $y=lg(x+1)+\frac{1}{lg(x+1)}$ | ||
| C. | $y=\sqrt{{x^2}+1}+\frac{1}{{\sqrt{{x^2}+1}}}$ | D. | $y=sinx+\frac{1}{sinx},({0<x<\frac{π}{2}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>1} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
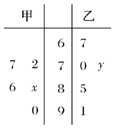 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com