已知集合A={(x,y)|x2+y2≤4},集合B={(x,y)|y≥m|x|,m为正常数}.若O为坐标原点,M,N为集合A所表示的平面区域与集合B所表示的平面区域的边界的交点,则△MON的面积S与m的关系式为 .
【答案】
分析:集合A={(x,y)|x
2+y
2≤4},集合B={(x,y)|y≥m|x|,m为正常数},在平面中作出A和B的图象,由此能求出平面区域的边界的交点,从而得到△MON的面积S与m的关系式.
解答: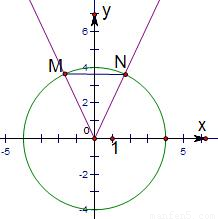
解:∵集合A={(x,y)|x
2+y
2≤4},表示一个圆内的部分;
集合B={(x,y)|y≥m|x|,m为正常数},表示角形区域部分;
在平面中作出A和B的边界的图象,
结合图象,知,集合A所表示的平面区域与集合B所表示的平面区域的边界的交点N,M的坐标分别为:N(
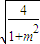
,m
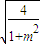
),M(-
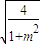
,m
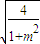
).
则△MON的面积S与m的关系式为S=

×(2
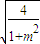
)×m
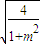
=
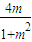
.
故答案为:
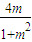
.
点评:本题考查二元一次不等式(组)与平面区域,解题时要认真审题,仔细解答,注意数形结合的合理运用.

 解:∵集合A={(x,y)|x2+y2≤4},表示一个圆内的部分;
解:∵集合A={(x,y)|x2+y2≤4},表示一个圆内的部分;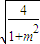 ,m
,m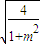 ),M(-
),M(-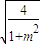 ,m
,m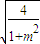 ).
). ×(2
×(2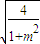 )×m
)×m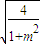 =
=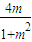 .
.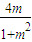 .
.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案