已知三次函数f(x)=ax3+bx2+cx+d(a、b、c、d∈R)为奇函数,且在点(1,f(1)) 的切线方程为y=2x-2.
(1)求函数f(x)的表达式.
(2)求曲线y=f(x)在点M(x0,f(x0))处的切线方程,并求曲线y=f(x)在点M(x0,f(x0))处的切线与曲线y=f(x)围成封闭图形的面积.
(3)如果过点(2,t)可作曲线y=f(x)的三条切线,求实数t的取值范围.
解:(1)f(-x)+f(x)=0,所以bx
2+d=0恒成立,
所以b=d=0,
所以f(x)=ax
3+cx,
又f′(x)=3ax
2+c,所以在点(1,f(1))的切线方程为y=(3a+c)(x-1)+a+c,即y=(3a+c)x-2a,
所以
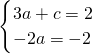
,解得
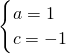
,
所以f(x)=x
3-x.
(2)解:设切点为(x
0,f(x
0)),f′(x)=3x
2-1,
则切线方程是:y=(
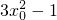
)(x-x
0)+(
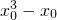
),
令x
3-x=(
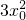
-1)(x-x
0)+(

-x
0),得

+2

=0,
所以(x-x
0)
2(x+2x
0)=0,所以曲线与切线的另一公共点的横坐标是-2x
0,
x
0>0时,S=
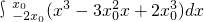
=(

x
4-
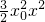
+2
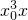
)

=
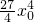
,
x
0<0时,S=-
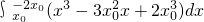
=
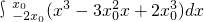
=
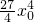
,
x
0=0时,切线与曲线恰有一个公共点,S=0=
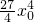
,
综上:曲线y=f(x)在点M(x
0,f(x
0))处的切线与曲线y=f(x)围成封闭图形的面积S=
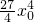
(x
0∈R).
(3)解:令切线过(2,t),代入整理得:

关于x
0有三个不同的解;
设g(x)=2x
3-6x
2+t+2,即g(x)有三个不同的零点;
又g′(x)=6x(x-2),
所以x∈(0,2)时g′(x)<0,g(x)递减;x∈(-∞,0)∪(2,+∞)时,g′(x)>0,g(x)在区间(-∞,0)∪(2,+∞)上分别递增,
故
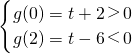
,解得-2<t<6.
所以实数t的取值范围为-2<t<6.
分析:(1)由奇函数得f(-x)+f(x)=0恒成立可求得b,d值,求出y=f(x)在点(1,f(1)) 的切线方程,对比y=2x-2的系数可求得a,c值;
(2)写出点M处切线方程,联立方程组求得另一交点横坐标分x
0>0时,x
0<0时,x
0=0时三种情况利用定积分即可求得;
(3)设切点为(x
0,f(x
0)),写出过点(2,t)的切线方程,问题转化为

关于x
0有三个不同的解,进而构造函数转化为函数有三个零点,利用导数求出极值,借助图形可得限制条件;
点评:本题考查利用导数求曲线的切线方程,考查定积分求图形面积,考查分类讨论思想,考查学生的转化能力.

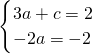 ,解得
,解得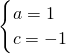 ,
,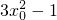 )(x-x0)+(
)(x-x0)+(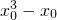 ),
),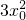 -1)(x-x0)+(
-1)(x-x0)+( -x0),得
-x0),得 +2
+2 =0,
=0,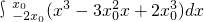 =(
=( x4-
x4-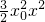 +2
+2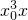 )
) =
=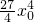 ,
,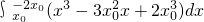 =
=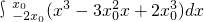 =
=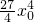 ,
,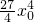 ,
,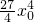 (x0∈R).
(x0∈R). 关于x0有三个不同的解;
关于x0有三个不同的解;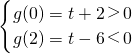 ,解得-2<t<6.
,解得-2<t<6. 关于x0有三个不同的解,进而构造函数转化为函数有三个零点,利用导数求出极值,借助图形可得限制条件;
关于x0有三个不同的解,进而构造函数转化为函数有三个零点,利用导数求出极值,借助图形可得限制条件;

 阅读快车系列答案
阅读快车系列答案