解:(1)当|t|<2时,由
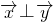
得:
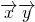
=-k+(t
2-3)t=0,
得k=f(t)=t
3-3t(|t|<2)
当|t|>2时,由
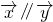
得:k=
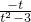
所以k=f(t)=

(5分)
(2)当|t|<2时,f′(t)=3t
2-3,由f′(t)<0,得3t
2-3<0
解得-1<t<1,
当|t|>2时,f′(t)=

=

>0
∴函数f(t)的单调递减区间是(-1,1).(4分)
(3)当|t|<2时,由f′(t)=3t
2-3=0得t=1或t=-1
∵1<|t|<2时,f′(t)>0
∴f(t)
极大值=f(-1)=2,f(t)
极小值=f(1)=-2
又f(2)=8-6=2,f(-2)=-8+6=-2
当t>2时,f(t)=
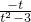
<0,
又由f′(t)>0知f(t)单调递增,∴f(t)>f(2)=-2,
即当t>2时,-2<f(t)<0,
同理可求,当t<-2时,有0<f(t)<2,
综合上述得,当t=-1或t=2时,f(t)取最大值2
当t=1或t=-2时,f(t)取最小值-2(5分)
分析:(1)利用向量垂直的充要条件及向量共线的充要条件列出关于k,t的方程,分离出k即为函数关系式k=f (t );
(2)分段求出函数的导函数,求出导函数小于0的x的范围,写出区间形式即得到函数f (t )的单调递减区间.
(3)利用(2)求出函数的极值.再求出区间的两个端点的函数值,选出最值.
点评:求分段函数的单调区间及极值、最值应该分段求,再选出最值.

 =(1,t2-3 ),
=(1,t2-3 ), =(-k,t) (其中实数k和t不同时为零),当|t|<2时,有
=(-k,t) (其中实数k和t不同时为零),当|t|<2时,有 ⊥
⊥ ,当|t|>2时,有
,当|t|>2时,有 ∥
∥ .
.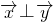 得:
得: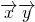 =-k+(t2-3)t=0,
=-k+(t2-3)t=0,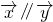 得:k=
得:k=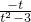
 (5分)
(5分) =
= >0
>0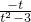 <0,
<0,
