
 如图5所示,在三棱锥
如图5所示,在三棱锥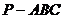 中,
中,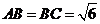 ,平面
,平面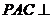 平面
平面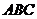 ,
,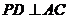 于点
于点 ,
,
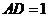 ,
,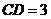 ,
,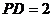 .
.
(1)求三棱锥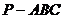 的体积;
的体积;
(2)证明△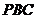 为直角三角形.
为直角三角形.
(本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)
(1)证明:因为平面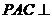 平面
平面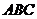 ,平面
,平面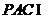 平面
平面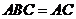 ,
,  平面
平面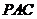 ,
, ,
,
所以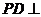 平面
平面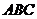 .…………………………………………………………………………………2分
.…………………………………………………………………………………2分
记 边上的中点为
边上的中点为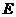 ,在△
,在△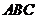 中,因为
中,因为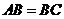 ,
,
所以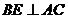 .
.
因为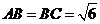 ,
,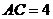 ,
,
所以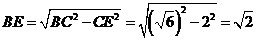 .………………………………………………………4分
.………………………………………………………4分
所以△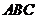 的面积
的面积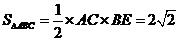 .……………………………………………………5分
.……………………………………………………5分
因为 ,
,
所以三棱锥 的体积
的体积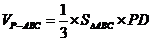
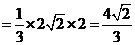 .……………………7分
.……………………7分
(2)证法1:因为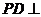
 ,所以△
,所以△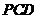 为直角三角形.
为直角三角形.
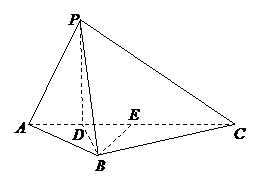 因为
因为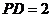 ,
,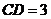 ,
,
所以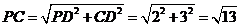 .………………9分
.………………9分
连接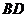 ,在
,在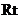 △
△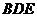 中,
中,
因为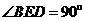 ,
,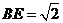 ,
,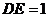 ,
,
所以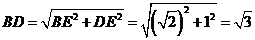 .…………10分
.…………10分
由(1)知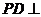 平面
平面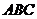 ,又
,又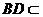 平面
平面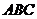 ,
,
所以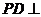
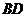 .
.
在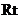 △
△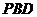 中,因为
中,因为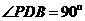 ,
,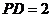 ,
,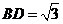 ,
,
所以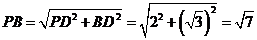 .……………………………………………………12分
.……………………………………………………12分
在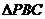 中,因为
中,因为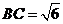 ,
,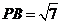 ,
,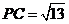 ,
,
所以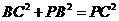 .………………………………………………………………………………13分
.………………………………………………………………………………13分
所以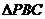 为直角三角形.……………………………………………………………………………14分
为直角三角形.……………………………………………………………………………14分
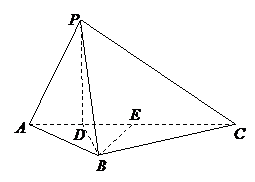 证法2:连接
证法2:连接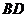 ,在
,在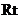 △
△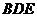 中,因为
中,因为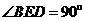 ,
,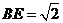 ,
,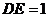 ,
,
所以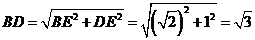 .…………8分
.…………8分
在△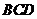 中,
中,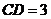 ,
,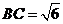 ,
,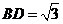 ,
,
所以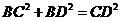 ,所以
,所以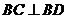 .………………10分
.………………10分
由(1)知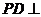 平面
平面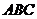 ,
,
因为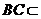 平面
平面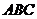 ,
,
所以 .
.
因为 ,
,
所以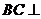 平面
平面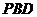 .…………………………………………………………………………………12分
.…………………………………………………………………………………12分
因为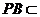 平面
平面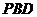 ,所以
,所以 .
.
所以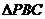 为直角三角形.……………………………………………………………………………14分
为直角三角形.……………………………………………………………………………14分


科目:高中数学 来源: 题型:
如图4,在边长为1的等边三角形![]() 中,
中,![]() 分别是
分别是![]() 边上的点,
边上的点,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起,得到如图5所示的三棱锥
折起,得到如图5所示的三棱锥![]() ,其中
,其中![]() .
.
 (1) 证明:
(1) 证明:![]() //平面
//平面![]() ;
;
(2) 证明:![]()
![]() 平面
平面![]() ;
;
(3) 当![]() 时,求三棱锥
时,求三棱锥![]() 的体积
的体积![]() .
.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省广州市高三综合测试(一)理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
如图5所示,在三棱锥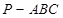 中,
中,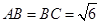 ,平面
,平面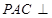 平面
平面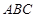 ,
,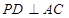 于点
于点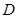 ,
,
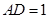 ,
,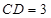 ,
,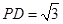 .
.
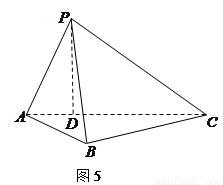
(1)证明△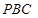 为直角三角形;
为直角三角形;
(2)求直线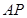 与平面
与平面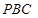 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
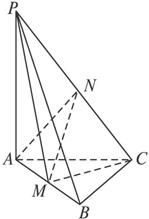
图5
(1)证明平面PAB⊥平面PCM;
(2)证明线段PC的中点为球O的球心;
(3)若球O的表面积为25π,求三棱锥P—ABC的体积.
查看答案和解析>>
科目:高中数学 来源:2012广州一模试题及答案(数学理) 题型:解答题
 如图5所示,在三棱锥
如图5所示,在三棱锥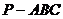 中,
中,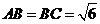 ,平面
,平面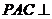 平面
平面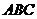 ,
,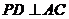 于点
于点 ,
,
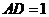 ,
,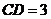 ,
,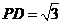 .
.
(1)证明△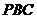 为直角三角形;
为直角三角形;
(2)求直线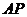 与平面
与平面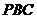 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com