
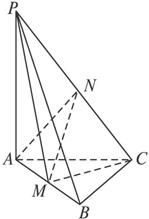
图5
(1)证明平面PAB⊥平面PCM;
(2)证明线段PC的中点为球O的球心;
(3)若球O的表面积为25π,求三棱锥P—ABC的体积.
(1)证明:∵AC=BC,M为AB的中点,
∴CM⊥AB.∵PA⊥平面ABC,CM![]() 平面ABC,∴PA⊥CM.
平面ABC,∴PA⊥CM.
∵AB∩PA=A,AB![]() 平面PAB,PA
平面PAB,PA![]() 平面PAB,∴CM⊥平面PAB.
平面PAB,∴CM⊥平面PAB.
∵CM![]() 平面PCM,∴平面PAB⊥平面PCM.
平面PCM,∴平面PAB⊥平面PCM.
(2)证明:由(1)知CM⊥平面PAB.

∵PM![]() 平面PAB,∴CM⊥PM.
平面PAB,∴CM⊥PM.
∵PA⊥平面ABC,AC![]() 平面ABC,∴PA⊥AC.
平面ABC,∴PA⊥AC.
取PC的中点N,连接MN、AN.
在Rt△PAC中,点N为斜边PC的中点,∴AN=PN=NC.
在Rt△PCM中,点N为斜边PC的中点.∴MN=PN=NC.
∴PN=NC=AN=MN.∴点N是球O的球心,即线段PC的中点为球O的球心.
(注:本题答案中符号“![]() ”等价于“
”等价于“![]() ”)
”)
(3)解:依题意得4π·NC2=25π,解得NC=![]() .
.
∴PC=5,PA=![]() =
=![]() =4.
=4.
∵AB=AC=BC=3,∴△ABC的面积S△ABC=![]() ×32=
×32=![]() .
.
∴三棱锥P—ABC的体积为V=![]() ×S△ABC×PA=
×S△ABC×PA=![]() ×
×![]() ×4=3
×4=3![]() .
.


科目:高中数学 来源: 题型:
如图4,在边长为1的等边三角形![]() 中,
中,![]() 分别是
分别是![]() 边上的点,
边上的点,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起,得到如图5所示的三棱锥
折起,得到如图5所示的三棱锥![]() ,其中
,其中![]() .
.
 (1) 证明:
(1) 证明:![]() //平面
//平面![]() ;
;
(2) 证明:![]()
![]() 平面
平面![]() ;
;
(3) 当![]() 时,求三棱锥
时,求三棱锥![]() 的体积
的体积![]() .
.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省广州市高三综合测试(一)理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
如图5所示,在三棱锥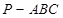 中,
中,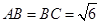 ,平面
,平面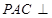 平面
平面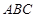 ,
,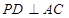 于点
于点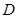 ,
,
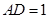 ,
,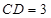 ,
,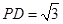 .
.
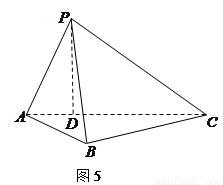
(1)证明△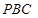 为直角三角形;
为直角三角形;
(2)求直线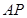 与平面
与平面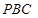 所成角的正弦值
所成角的正弦值
查看答案和解析>>
科目:高中数学 来源:2012广州一模试题及答案(数学理) 题型:解答题
 如图5所示,在三棱锥
如图5所示,在三棱锥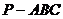 中,
中,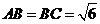 ,平面
,平面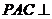 平面
平面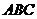 ,
,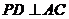 于点
于点 ,
,
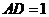 ,
,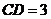 ,
,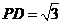 .
.
(1)证明△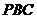 为直角三角形;
为直角三角形;
(2)求直线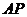 与平面
与平面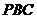 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com