练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在中,根据下列条件解三角形,其中有两个解的是（ ）

    A. b="10," A=450, C=600 B. a=6, c=5, B=600

    C. a=7, b=5, A=600 D. a=14, b="16," A=450

    【答案】C

    【解析】试题分析：解：A、∵A=45°，C=70°，∴B=65°，又b=10，

    ∴由正弦定理得，此时三角形只有一解，不合题意；

    B、∵a=60，c=48，B=60°，∴由余弦定理得：，

    ∴此时三角形有一解，不合题意；

    C、∵a=7，b=5，A=80°，∴由正弦定理得，又b＜a，∴B＜A=80°，

    ∴B只有一解，不合题意；

    D、∵a=14，b=16，A=45°，∴由正弦定理得，∵a＜b，

    ∴45°=A＜B，∴B有两解，符合题意，故选D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某市春节期间7家超市的广告费支出（万元）和销售额（万元）数据如下：

    超市

    A

    B

    C

    D

    E

    F

    G

    广告费支出

    1

    2

    4

    6

    11

    13

    19

    销售额

    19

    32

    40

    44

    52

    53

    54

    （1）若用线性回归模型拟合与的关系，求关于的线性回归方程；

    （2）用二次函数回归模型拟合与的关系，可得回归方程：，

    经计算二次函数回归模型和线性回归模型的分别约为和，请用说明选择哪个回归模型更合适，并用此模型预测超市广告费支出为3万元时的销售额．

    参数数据及公式：，，

    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】【2016高考山东理数】已知.

    （I）讨论的单调性；

    （II）当时，证明对于任意的成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (Ⅰ)若,令函数,求函数在上的极大值、极小值；

    (Ⅱ)若函数在上恒为单调递增函数,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝x－1＋x2－2，试利用基本初等函数的图象，判断f(x)有几个零点，并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为2.10元，当用水超过4吨时，超过部分每吨3.00元，某月甲、乙两户共交水费y元．已知甲、乙两用户该月用水量分别为5x,3x吨．

    (1)求y关于x的函数；

    (2)如甲、乙两户该月共交水费40.8元，分别求出甲、乙两户该月的用水量和水费．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知（）．

    （Ⅰ）求证：；

    （Ⅱ）若不等式在时恒成立，求最小正整数，并给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，用K、A1、A2三类不同的元件连接成一个系统．当K正常工作且A1、A2至少有一个正常工作时，系统正常工作，已知K、A1、A2正常工作的概率依次是0.9、0.8、0.8，则系统正常工作的概率为（ ）

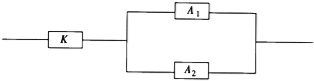
    A. 0.960 B. 0.864 C. 0.720 D. 0.576

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知设函数 ．

    （1）求 的定义域；

    （2）判断 的奇偶性并予以证明；

    （3）求使 的 的取值范围．

    查看答案和解析>>

    同步练习册答案