【答案】
分析:A:(I)本题考查矩阵的特征值及特征向量,先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
(II)对某个向量连续施行多次变化的计算;
B:将直线的参数方程化成普通方程为x+2y=0,并设椭圆上任一点P为(2cosθ,sinθ),则可根据点到直线的距离公式得到:P到直线l的距离是一个关于θ的函数,即可求解
解答:A解:(Ⅰ)矩阵A的特征多项式为:f(λ)=

=λ
2-5λ+6=0
得:λ
1=2,λ
2=3,当λ
1=2时,解得α
1=(2,1)
当λ
2=3时,解得α
2=(1,1).
(Ⅱ)由α=mα
1+nα
2得

解得:

由(2)得:A
5α=A
5(3α
1+α
2)=3(A
5α
1)+A
5α
2=3(λ
15α
1)+λ
25α
2=3×2
5×(2,1)+3
5×(1,1)=(435,339)
B.坐标系与参数方程
解:直线l的参数方程为

(t为参数)故直线l的普通方程为x+2y=0
因为p为椭圆

上任意点,故可设P(2cosθ,sinθ)其中θ∈R.
因此点P到直线l的距离是

所以当

,k∈z时,d取得最大值

.
点评:本题考查了二阶矩阵,直线的参数方程,直线与圆锥曲线的综合问题属于基础题.

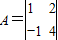 ,向量
,向量 =
= .
. (t为参数),P是椭圆
(t为参数),P是椭圆 上任意一点,求点P到直线l的距离的最大值.
上任意一点,求点P到直线l的距离的最大值. =λ2-5λ+6=0
=λ2-5λ+6=0

 (t为参数)故直线l的普通方程为x+2y=0
(t为参数)故直线l的普通方程为x+2y=0 上任意点,故可设P(2cosθ,sinθ)其中θ∈R.
上任意点,故可设P(2cosθ,sinθ)其中θ∈R.
 ,k∈z时,d取得最大值
,k∈z时,d取得最大值 .
.

 (2012•江苏二模)选做题
(2012•江苏二模)选做题
 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
; 的最大值.
的最大值.