
 已知函数
已知函数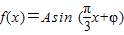 ,x∈R,A>0,
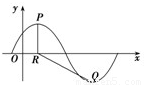
,x∈R,A>0,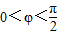 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).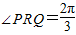 ,求A的值.
,求A的值.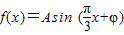 ,我们易求出函数的最小正周期,又由P的坐标为(1,A),我们易构造出一个关于φ的三角方程,结合
,我们易求出函数的最小正周期,又由P的坐标为(1,A),我们易构造出一个关于φ的三角方程,结合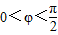 解三角方程即可求出φ值.
解三角方程即可求出φ值. ,利用余弦定理我们易构造出一个关于A的方程,解方程即可得到A的值.
,利用余弦定理我们易构造出一个关于A的方程,解方程即可得到A的值. =6
=6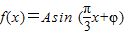 的图象上
的图象上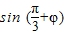 =1
=1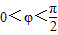
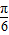
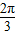
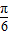 ,作QM⊥X轴于M,则QM=A,RM=3,
,作QM⊥X轴于M,则QM=A,RM=3,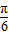 =
=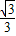 =
=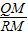 =
=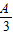
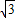


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:专项题 题型:解答题
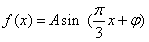 ,x∈R,A>0,
,x∈R,A>0,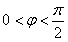 。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。
。y=f(x)部分图象如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A)。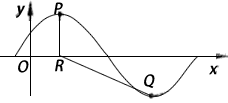
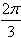 ,求A的值。
,求A的值。查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省永州市祁阳四中高三(上)段考数学试卷(文科)(解析版) 题型:解答题
 已知函数
已知函数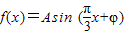 ,x∈R,A>0,
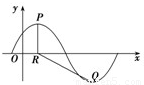
,x∈R,A>0,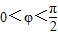 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).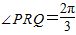 ,求A的值.
,求A的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省数学试卷双流市棠中外语学校高三(上)9月月考数学试卷(文科)(解析版) 题型:解答题
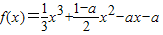 ,x∈R其中a>0.
,x∈R其中a>0.查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市源清中学高一(下)数学暑假作业(三角函数)(解析版) 题型:解答题
 已知函数
已知函数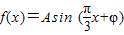 ,x∈R,A>0,
,x∈R,A>0,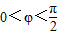 .y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).
.y=f(x)的部分图象,如图所示,P、Q分别为该图象的最高点和最低点,点P的坐标为(1,A).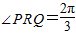 ,求A的值.
,求A的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com