
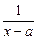 (2) a的取值范围是0<a≤
(2) a的取值范围是0<a≤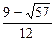
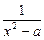 ,∴g(x)=loga
,∴g(x)=loga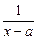 .
. 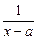 =
=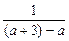 >0,
>0,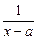 |
| f(x)=x2-4ax+3a2在[a+2,a+3]上为减函数,
f(x)=x2-4ax+3a2在[a+2,a+3]上为减函数,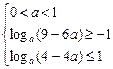 的解.
的解. 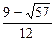 ,
,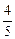 ,
,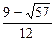 .
. 

科目:高中数学 来源:不详 题型:解答题
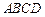 中,已知
中,已知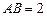 ,
,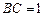 ,在
,在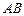 .
.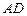 .
.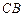 .
.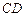 上,分别截取
上,分别截取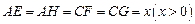 ,设四边形
,设四边形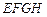 的面积为
的面积为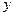 .
.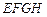 的面积
的面积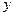 与
与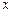 之间的函数关系式;
之间的函数关系式;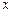 为何值时
为何值时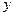 取得最大值,最大值是多少?
取得最大值,最大值是多少?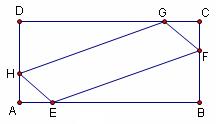
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
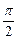 ],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
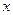 (单位:元,
(单位:元,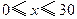 )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.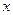 的函数;
的函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 给出下列结论:①f (x)是奇函数;②f (x)在(-1,1)内是增函数;③
给出下列结论:①f (x)是奇函数;②f (x)在(-1,1)内是增函数;③ 。试判断这些结论的正确性,并说明理由。
。试判断这些结论的正确性,并说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com