练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若{an}是各项都大于零的等比数列，且公比q≠1，则a1＋a4与a2＋a3的大小关系是

    [　　]

    A．a1＋a4＜a2＋a3

    B．a1＋a4＞a2＋a3

    C．a1＋a4＝a2＋a3

    D．不确定

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a2+b3=a3+b2=7．
    （1）求{an}，{bn}的通项公式；
    （2）记cn=an-2010，n∈N*，An为数列{cn}的前n项和，当n为多少时An取得最大值或最小值？
    （3）（理）是否存在正数K，使得(1+
    1
    a1
    )(1+
    1
    a2
    )…(1+
    1
    an
    )≥K
    		2n+1
    对一切n∈N*均成立，若存在，求出K的最大值，若不存在，说明理由．
    （4）（文）求数列{
    an
    bn
    }    的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知各项均为正数的数列{an}中，a1=1，Sn是数列{an}的前n项和，对任意n∈N*，有2Sn=2pan2+pan-p（p∈R）．
    （1）求常数p的值；  
    （2）求数列{an}的通项公式；
    （3）记bn=Sn+λan，（n∈N*）若数列{bn}从第二项起每一项都比它的前一项大，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2014届辽宁沈阳四校协作体高二上学期期中考试理数学试卷（解析版） 题型：填空题

    无穷等差数列{an}各项都是正数，Sn是它的前n项和，若a1+a3+a8=a42,则a5·S4的最大值是______________.

     

    查看答案和解析>>

    科目：高中数学 来源：2007-2008学年江苏省无锡一中高三（上）期中数学试卷（解析版） 题型：解答题

    已知各项均为正数的数列{an}中，a1=1，Sn是数列{an}的前n项和，对任意n∈N*，有2Sn=2pan2+pan-p（p∈R）．
    （1）求常数p的值；  
    （2）求数列{an}的通项公式；
    （3）记bn=Sn+λan，（n∈N*）若数列{bn}从第二项起每一项都比它的前一项大，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2011年上海市静安区高考数学一模试卷（文理合卷）（解析版） 题型：解答题

    设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a2+b3=a3+b2=7．
    （1）求{an}，{bn}的通项公式；
    （2）记cn=an-2010，n∈N*，An为数列{cn}的前n项和，当n为多少时An取得最大值或最小值？
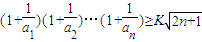    （3）（理）是否存在正数K，使得对一切n∈N*均成立，若存在，求出K的最大值，若不存在，说明理由．
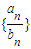    （4）（文）求数列的前n项和Sn．

    查看答案和解析>>

    同步练习册答案