�⣺��1��������ɵá�����������{
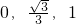
}�ĺ���Ϊy=
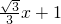
��
��ͼ������ƽ��2����λ���õ����º����Ľ���ʽ��y=
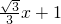
-2����y=
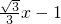
��
��2���������֪y=
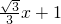
����ƽ��������λ��y=
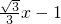
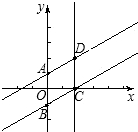
��AD��BC����AB=2����ֱ�ߵķ��̿�֪AB��CD��
���ı���ABCDΪƽ���ı��Σ�
ͬʱ�ɵ�C������Ϊ��

��0����D��

��2��
�ɹ��ɶ����ɵ�BC=2����AB=BC=2
���ı���ABCDΪ���Σ�
��3���ɵö��κ���Ϊ��y=x
2-2bx+b
2+

����Ϊ����ʽΪ��y=��x-b��
2+

��
����κ�����ͼ�ᾭ����B�͵�C��
����κ�����ͼ�����ı����й������֣�
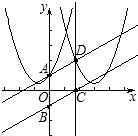
�����κ�����ͼ����Aʱ����A��0��1����������κ�����
���b=-

��b=

���������⣬��ȥ����
�����κ�����ͼ����Dʱ����D��

��2��������������
���b=

+

��b=
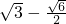
���������⣬��ȥ����
����ʵ��b��ȡֵ��Χ��
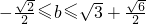
��
��������1��������ɵú�������ʽ����ƽ�Ƶ�֪ʶ�ɵã�
��2����ֱ�ߵķ�����֤�ı���Ϊƽ���ı��Σ�������ɵ�AB=BC���������Σ�
��3���ֱ���ú���ͼ�����A��Dʱ��bֵ�����ν�Ͽɵ÷�Χ��
���������⿼���¶��壬�漰���κ�����ֱ�ߵ�λ�ù�ϵ���ж����������⣮

 ����{a��b��c}Ϊ����y=ax2+bx+c�ġ������������磺����y=x2-2x+3�ġ�����������{1��-2��3}������y=2x+3�ġ�����������{0��2��3��}������y=-x�ġ�����������{0��-1��0}
����{a��b��c}Ϊ����y=ax2+bx+c�ġ������������磺����y=x2-2x+3�ġ�����������{1��-2��3}������y=2x+3�ġ�����������{0��2��3��}������y=-x�ġ�����������{0��-1��0}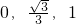 }�ĺ���ͼ������ƽ��2����λ���õ����º����Ľ���ʽ��________�� ����д�ڴ���ϣ�
}�ĺ���ͼ������ƽ��2����λ���õ����º����Ľ���ʽ��________�� ����д�ڴ���ϣ� �ֱ���D��C���㣬��ƽ��ֱ������ϵ�л���ͼ�Σ��ж��Ե�A��B��C��DΪ������ı�����״����˵�����ɣ�
�ֱ���D��C���㣬��ƽ��ֱ������ϵ�л���ͼ�Σ��ж��Ե�A��B��C��DΪ������ı�����״����˵�����ɣ� }�ĺ���ͼ����н��㣬������������ʵ��b��ȡֵ��Χ��
}�ĺ���ͼ����н��㣬������������ʵ��b��ȡֵ��Χ��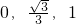 }�ĺ���Ϊy=
}�ĺ���Ϊy=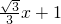 ��
��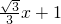 -2����y=
-2����y=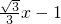 ��
��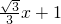 ����ƽ��������λ��y=
����ƽ��������λ��y=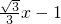

 ��0����D��
��0����D�� ��2��
��2�� ����Ϊ����ʽΪ��y=��x-b��2+
����Ϊ����ʽΪ��y=��x-b��2+ ��
��
 ��b=
��b= ���������⣬��ȥ����
���������⣬��ȥ���� ��2����������κ�����
��2�������������� +
+ ��b=
��b=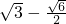 ���������⣬��ȥ����
���������⣬��ȥ����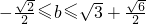 ��
��

 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д� ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
 ����{a��b��c}Ϊ����y=ax2+bx+c�ġ������������磺����y=x2-2x+3�ġ�����������{1��-2��3}������y=2x+3�ġ�����������{0��2��3��}������y=-x�ġ�����������{0��-1��0}
����{a��b��c}Ϊ����y=ax2+bx+c�ġ������������磺����y=x2-2x+3�ġ�����������{1��-2��3}������y=2x+3�ġ�����������{0��2��3��}������y=-x�ġ�����������{0��-1��0}