
某加工厂用某原料由甲车间加工出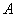 产品,由乙车间加工出
产品,由乙车间加工出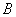 产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克
产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克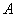 产品,每千克
产品,每千克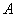 产品获利50元.乙车间加工一箱原料需耗费工时6小时可加工出4千克
产品获利50元.乙车间加工一箱原料需耗费工时6小时可加工出4千克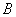 产品,每千克
产品,每千克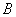 产品获利60元.甲、乙两车间每天共能完成至多80箱原料的加工,每天甲、乙车间耗费工时总和不得超过600小时。
产品获利60元.甲、乙两车间每天共能完成至多80箱原料的加工,每天甲、乙车间耗费工时总和不得超过600小时。
(1)若安排甲、乙两车间每天分别加工20箱和40箱原料,则甲、乙两车间每天共获利多少元?
(2)问应如何安排生产,才能使甲、乙两车间每天获利的总和最大

 ?
?
科目:高中数学 来源: 题型:
关于平面向量a,b,c,有下列三个命题:
①若a·b=a·c,则b=c;②若a=(1,k),b=(-2,6),a∥b,则k=-3;③非零向量a和b满足|a|=|b|=|a-b|,则a与a+b的夹角为60°.
其中真命题的序号为_______.(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com