甲乙各自都有一个放有3个红球.2个白球.1个黄球共6个球的箱子.(1)若甲在自己的箱子中任意取球.取后不放回. 每次只取1个.直到取出红球为止.求甲取球的次数的分布列和数学期望.(2)若甲乙各自从自己的箱子中任取一个球比颜色.规定同色时甲胜.异色时乙胜.这种游戏规则公平吗?请说明理由. 题目和参考答案——青夏教育精英家教网—

甲乙各自都有一个放有3个红球，2个白球，1个黄球共6个球的箱子.
（1）若甲在自己的箱子中任意取球，取后不放回. 每次只

取1个，直到取出红球为止，求甲取球的次数

的分布列和数学期望.
（2）若甲乙各自从自己的箱子中任取一个球比颜色，规定同色时甲胜，异色时乙胜，这种游戏规则公平吗？请说明理由.

（1）略
（2）不公平

(1)

x	1	2	3	4
p

(2)甲获胜的概率

所以规则不公平

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：不详 题型：解答题

在我市“城乡清洁工程”建设活动中，社会各界掀起净化美化环境的热潮.某单位计划在小区内种植

四棵风景树，受本地地理环境的影响，

两棵树的成活的概率均为

，另外两棵树

为进口树种，其成活概率都为

，设

表示最终成活的树的数量.
（1）若出现

有且只有一颗成活的概率与

都成活的概率相等，求

的值；
（2）求

的分布列（用

表示）；
（3）若出现恰好两棵树成活的的概率最大，试求

的取值范围.

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

（本题12分）
有一种舞台灯，外形是正六棱柱，在其每一个侧面

(编号为①②③④⑤⑥)上安装5只颜色各异的灯，假若每只灯正常发光的概率为0.5，若一个侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用

表示更换的面数，用

表示更换费用。
（1）求①号面需要更换的概率；
（2）求6个面中恰好有2个面需要更换的概率；
（3）写出

的分布列，求

的数学期望。

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

（本题满分14分）在一种智力有奖竞猜游戏中，每个参加者可以回答两个问题（题1和题2），且对两个问题可以按自己选择的顺序进行作答，但是只有答对了第一个问题之后才能回答第二个问题。假设：答对题

（

），就得到奖金

元，且答对题

的概率为

（

），并且两次作答不会相互影响．
（I）当

元，

，

元，

时，某人选择先回答题1，设获得奖金为

，求

的分布列和

；
（II）若

，

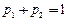，试问：选择先回答哪个问题时可能得到的奖金更多？

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

（本小题满分12分）
从某学校高三年级共800名男生中随机抽取50名测量身高，测量发现被测学生身高全部介于155 cm和195 cm之间，将测量结果按如下方式分成八组：第一组[155,160)、第二组[160,165)、…、第八组[190,195]，下图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组、第七组、第八组人数依次构成等差数列．