
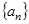 的前
的前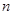 项和
项和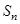 满足
满足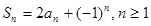 .
.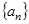 的前三项
的前三项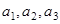 ;
;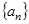 的通项公式;
的通项公式;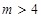 ,有
,有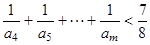 .
.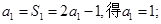 由
由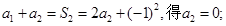
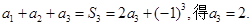
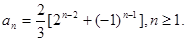
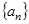 的前
的前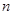 项和
项和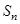 满足
满足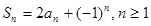 ,那么对于n令值,边可以写出数列
,那么对于n令值,边可以写出数列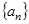 的前三项
的前三项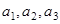 ;
;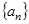 的通项公式;再用数学归纳法加以证明。或者里利用迭代思想
的通项公式;再用数学归纳法加以证明。或者里利用迭代思想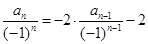 ,得到通项公式。
,得到通项公式。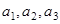 的值,只要在递推式
的值,只要在递推式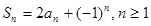 中,对
中,对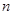 取特殊值
取特殊值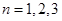 ,就可以消除解题目标与题设条件之间的差异.
,就可以消除解题目标与题设条件之间的差异.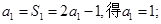
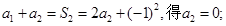
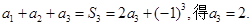
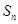 .事实上
.事实上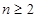 时,有
时,有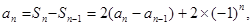

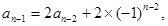
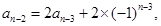
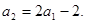
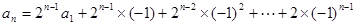
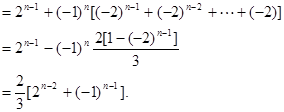
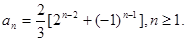
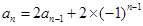 和课本习题
和课本习题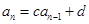 作联系,容易想到:这种差异的消除,只要对
作联系,容易想到:这种差异的消除,只要对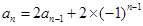 的两边同除以
的两边同除以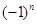 ,便得
,便得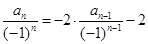 .
.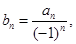 就有
就有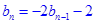 ,
,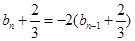 ,
,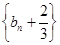 是等比数列,公比
是等比数列,公比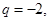 首项
首项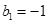 ,从而,得
,从而,得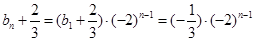 ,
,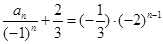 ,
,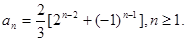
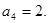
 且n为奇数时,
且n为奇数时, 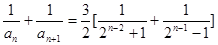
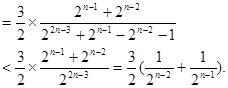
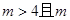 为偶数时,
为偶数时,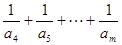
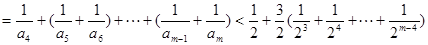
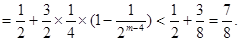
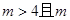 为奇数时,
为奇数时,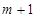 为偶数,可以转化为上面的情景
为偶数,可以转化为上面的情景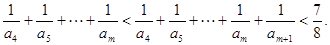
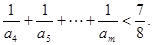


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源:不详 题型:解答题
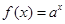 (
(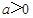 且
且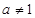 )的图象上,等比数列
)的图象上,等比数列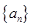 的前
的前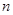 项和为
项和为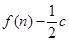 ,数列
,数列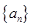
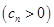 的首项为c,且其前
的首项为c,且其前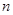 项和
项和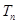 满足 2
满足 2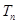 =
=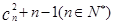 .
.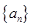 和
和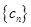 的通项公式;
的通项公式;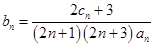 ,求数列
,求数列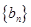 的前
的前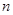 项和
项和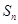 .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
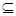 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com